This mathematics ClipArt gallery offers 87 illustrations of analytical geometry, which is also called coordinate geometry, Cartesian geometry, algebraic geometry, or simply analytic geometry. It is the study of geometry using principles of algebra.
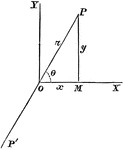
Rectangular Axes
Transforming from one set of rectangular axes to another with the same origin, but different direction.
Periodic Center of Motion
Illustration showing the periodic center of motion as it often happens when two positions of a line…

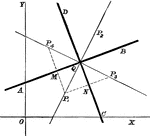
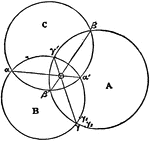
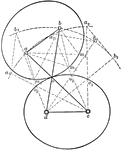
Centrodes
Aronhold stated if any three bodies have plane motion their three virtual centers are three points on…
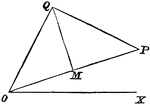
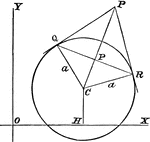
Centroid
Illustration showing a centroid, "the curve passing through the successive positions of the instantaneous…
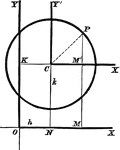
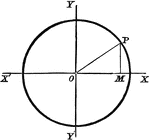
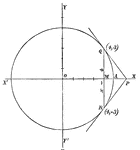
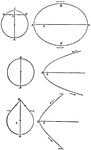
Common Form of Circle
A circle in its common, or central form. This is used to assist students in finding the equation of…
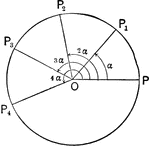
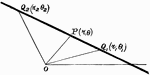
Geometric Inspection of Complex Numbers
Illustration showing complex numbers with a modulus equal to unity. The lines representing these numbers…
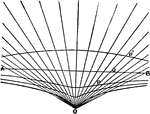
Conchoid
Illustration showing a conchoid, "a curve, shell-like in flexure (whence the name), invented by Nicomedes…
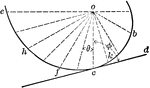
Motion of Open Curves
"Since these curves are not closed, one pair cannot be used for continuous motion; but a pair of such…
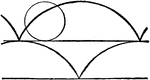
Cycloid
Illustration showing a cycloid curve. "The curve generated by a point in the plane of a circle when…
Cycloid
Illustration showing a cycloid curve. "The curve generated by a point in the plane of a circle when…
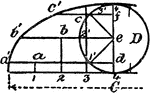
Construction Of A Cycloid
An illustration showing how to construct a cycloid. "The circumference C=3.14D. Divide the rolling circle…

Cycloids
Illustration showing cycloid curves. "The curve generated by a point in the plane of a circle when the…
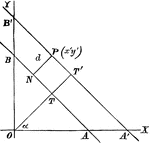
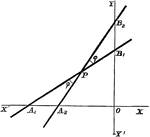
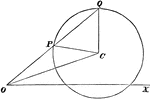
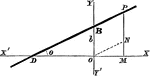
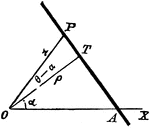
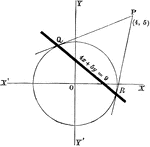
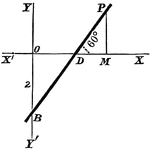
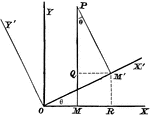
Perpendicular Distance
Finding the perpendicular distance of points whose equation is x cosa + y sina = p.

Ellipsoid
Each section is an ellipse. The surface is generated by an ellipse moving parallel to itself along two…
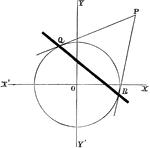
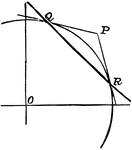
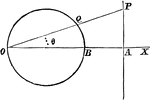
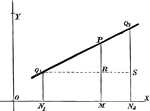
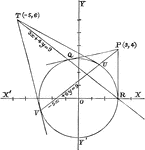
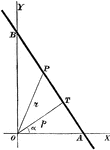
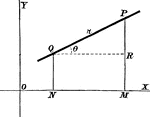
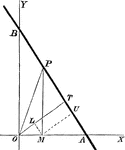
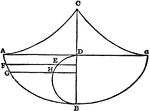
Chord Equation
Tangent lines are drawn from a given external point to a circle. The equation is found by joining their…

Construction Of An Evolute Of A Circle
An illustration showing how to construct an evolute of a circle. "Given the pitch p, the angle v, and…

Folium of Descartes
"Folium of Descartes, with its asymptote. The equation is (4-y)(y-1)2 = 3x2y ... In geometry, a plane…
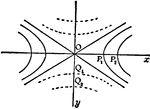
Hyperbolic Parabaloid
Three dimensional representation of a variable hyperbola moving parallel to itself along the parabolas…
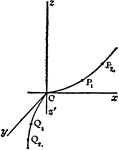
Hyperbolic Parabaloid
Two dimensional representation of variable hyperbola moving parallel to itself along the parabolas as…
Construction Using Isometric Perspective
An illustration showing how to use isometric perspective. "This kind of perspective admits of scale…
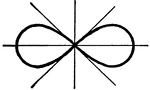
Lemniscate
A Lemniscate is, in general, a curve generated by a point moving so that the product of its distances…

Motions Of 2 Points In Same Plane And Parallel
Illustration showing two points a and b to be in the same plane and parallel.
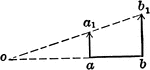
Motions Of 2 Points In Same Plane And Parallel
Illustration showing two points a and b to be in the same plane and parallel.
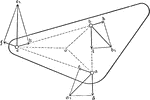
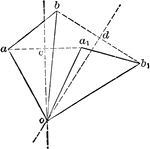
Motions Of 3 Points
Illustration showing three points a, b, and c in motion. The magnitude and direction of a and b are…
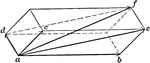
Parallelopiped of Motions
Illustration used "If three component motions ab, ac, and ad are combined, their resultant af will be…