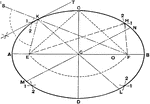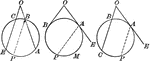
Circles With Angles Formed by Secants and Tangents
Illustration showing angles formed by two secants, two tangents, or a tangent and a secant, drawn to…
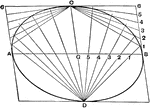
Intersecting Lines in Circles
Illustration showing various circles and the angles formed by intersecting lines.
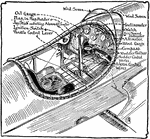
Aeroplane Cockpit
A pilot's cockpit from a propeller aeroplane, or airplane. The diagram illustrates the different parts…

Dipping Compass
An instrument consisting essentially of a dipping needle, a verticle graduated circle whose center coincides…
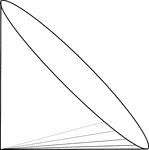
Right Circular Cone on Side
Illustration of a right circular cone resting on an element such that the vertex is on the bottom and…
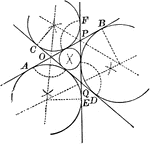
Construction of Escribed Circles With Ex-centres
Illustration of the construction used to escribe circles with centres (centers) called ex-centres of…
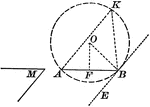
Construction to Describe a Segment of a Circle in Which an Angle Can Be Inscribed
Illustration of the construction used upon a given straight line, to describe a segment of a circle…
Construction of a Triangle When Given a Side and Two Angles
Illustration of the construction used to make a triangle when given a side and two angles.
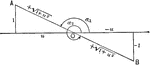
Negative Cotangent Angles
Illustration that can be used to show that if the cotangent of an angle is negative the angle must terminate…
Curve in Pavement of Road
Illustration of blueprint used by highway engineers to widen the pavement on the inside of the curve…

Angle of Depression
Illustration showing an angle of depression from a horizontal line to a line of sight.

Aeroplane High Tail Normal Attitude Design
A design of the propeller airplane, or aeroplane, in flight with a higher tail to create an angle of…

Aeroplane High Tail Slow Landing Design
A propeller airplane, or aeroplane, design with a high tail. This design creates a larger angle of incidence…

Aeroplane Low Tail Design
Illustration of a propeller aeroplane, or airplane, with lower tail in flight.
Aeroplane Low Tail Fast Landing Design
The propeller airplane, or aeroplane, design in fast landing. This design requires a large landing area…
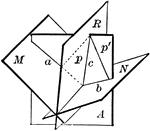
Plane Bisecting Dihedral Angle
Diagram used to prove the theorem: "Every point in a plane which bisects a dihedral angle is equidistant…
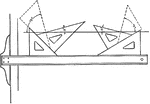
Drawing Lines using Triangle at Angles in Multiples of 15 degrees
The 45-degree triangle can be used to make a line at a multiple of 15 degrees.
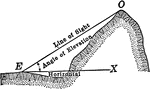
Angle of Elevation
Illustration showing an angle of elevation from a horizontal line to a line of sight.
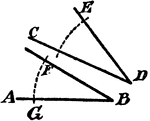
Construction Of An Equal Angle
An illustration showing the construction used to erect an equal angle. "With D as a center, draw the…

Airplane Flying Above Land
A plane flying above land illustrating the use of ailerons to adjust the angle of incidence to adjust…

Airplane Flying Above Shore
An airplane flying above the show illustrating the aerodynamics of the plane with the tail wing at the…

Aeroplane Flying Over Plane
An illustration of the plane flying over land from point A to B by flying the plane with the direction…
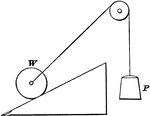
Inclined Plane with Force at an Angle to Plane and Base
"An inclined plane is a slope, or a flat surface, making an angle with a horizontal line...the force…
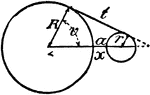
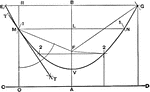
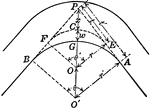
Model Of Geometric Relationships In 2 Circles
An illustration showing a model of 2 circles with tangent lines, diameters, and radii that illustrates…
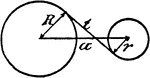
Model Of Geometric Relationships In 2 Circles
An illustration showing a model of 2 circles with tangent lines, diameters, and radii that illustrates…
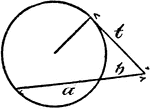
Model Of Geometric Relationships In A Circle
An illustration showing a model of a circle with an exterior angle formed between a tangent and a secant…
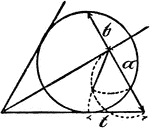
Model Of Geometric Relationships In A Circle
An illustration showing a model of a circle with angles formed between tangents and secants that illustrates…
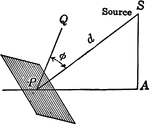
Illumination of a Surface When the Surface is not Perpendicular to the Source
Illustration modeling the illumination on a surface when the surface is not perpendicular to hte rays…
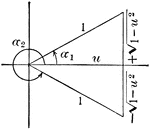
Angle Expressed As An Inverse Function
Illustration that can be used to show that when given an angle, expressed as an inverse function of…
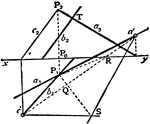
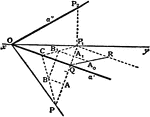
Angle of Two Lines
To find the angle between two given lines a, b of which the projections a1, b1 and a2, b2 are given.
Perpendicular Line Drawn To a Given Line From an External Point
Illustration showing that the perpendicular is the shortest line that can be drawn to a straight line…
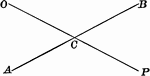
Intersecting Straight Lines
Illustration of two lines intersecting at a point. This can be used to show vertical angles.
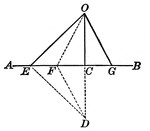
Lines Drawn From the Same Point in a Perpendicular to a Given line, Cutting Off Segments
Illustration showing two straight lines drawn from the same point in a perpendicular to a given line,…
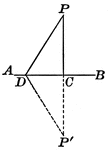
Lines Drawn From the Point C to the Extremities of the Straight line AB
Illustration showing two lines CA and CB drawn from the point C to the extremities of the straight line…
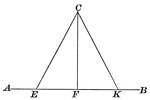
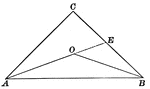
Lines Drawn to Another Line to Form Triangle
Illustration of two straight lines drawn from a point in a perpendicular to a given line, cutting off…
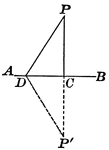
Perpendicular Line Drawn to a Given Line from an External Point
Illustration showing only one perpendicular can be drawn to a given line from a given external point.
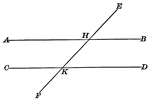
Parallel Lines Cut By A Transversal
Illustration showing that when two parallel lines are cut by a transversal, the exterior-interior angles…
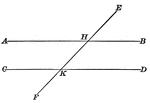
Parallel Lines Cut By A Transversal
Illustration showing that when two parallel lines are cut by a transversal, the two interior angles…
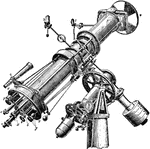
Micrometer
"The circles for position angle and declination are read by micrometer microscopes illuminated by the…

Regular Pentagon With Circle Inscribed
Illustration showing a circle inscribed in a regular pentagon. Or, a regular pentagon circumscribed…
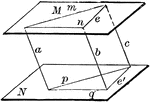
Angles In Parallel Planes
"If two angles not in the same plane have their sides respectively parallel and lying in the same direction,…
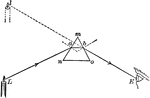
Prism
"A prism is a transparent body with two refraction surfaces that lie in intersecting planes. The angle…
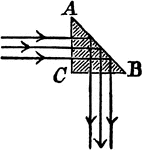
Cathetal Prism
"Cathetal prisms readily yield the phenomena of total reflection as shown, and are often used when light…
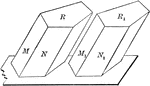
Two Equal Prisms
Diagram used to prove the theorem: "Two prisms are equal when the three faces about a trihedral of one…