Clipart tagged: ‘height’
Barometer Measuring Pressure of a Partially Evacuated Vessel
"The degree to which the air has been exhausted from a closed vessel in which there is a partial vacuum…
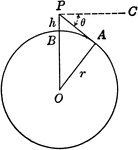
Circle With Center o and Radius r with point P
Circle modeling the earth. O is the center of the earth, r the radius of the earth, and h the height…

Right Circular Cone With 2 ft. Height and 1 ft. Radius
An illustration of a right circular cone with la radius of 1 foot and a height of 2 feet. Illustration…
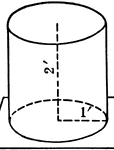
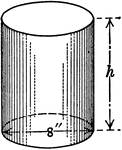
Right Circular Cylinder With 1 ft. Radius and 2 ft. height.
Right circular cylinder with a radius of 1 foot and a height/altitude of 2 feet.
Construction Of Equilateral Triangle
Illustration used to show how to draw an equilateral triangle when given the altitude.

Girl Measuring Heights of Children
An illustration of a girl measuring the heights of a boy and girl.
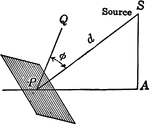
Illumination of a Surface When the Surface is not Perpendicular to the Source
Illustration modeling the illumination on a surface when the surface is not perpendicular to hte rays…
Kauri Pine
The Kauri Pine (Agathis australis) is a coniferous tree peculiar to New Zealand, and forming its most…

Levelling
Leveling is an operation in which the object is to determine to difference of vertical height between…
Area of a Parallelogram
Illustration of parallelogram AEFC drawn two different ways with base b and altitude/height a used to…

Parallelogram With Dimensions
Parallelogram with dimensions labeled. Parallelogram can be used to calculate area.

Parallelogram With Dimensions
Parallelogram with dimensions labeled. Parallelogram can be used to calculate area.
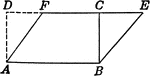
Parallelogram and Rectangle Relationship
Parallelogram with dimensions drawn to show relationship to the area of a rectangle.

Pentagon With Triangular Sections For Area
Pentagon with dimensions labeled. Pentagon can be used to calculate area by calculating individual triangles…
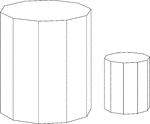
Similar Decagonal Prisms
Illustration of 2 similar right decagonal prisms. Both have regular decagons for bases and rectangular…
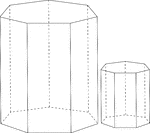
Similar Heptagonal/Septagonal Prisms
Illustration of 2 similar right heptagonal/septagonal prisms. Both have regular heptagons/septagons…

Similar Hexagonal Prisms
Illustration of 2 similar right hexagonal prisms. The height of the prism and length of the side of…
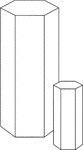
Similar Hexagonal Prisms
Illustration of 2 similar right hexagonal prisms. The height of the prism and length of the side of…
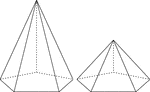
2 Right Pentagonal Pyramids
Illustration of 2 right pentagonal pyramids with hidden edges shown. The pentagonal bases are congruent,…
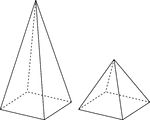
2 Right Rectangular Pyramids
Illustration of 2 right rectangular pyramids with hidden edges shown. The rectangular bases are congruent,…
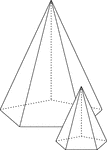
Similar Pentagonal Pyramids
Illustration of 2 similar right pentagonal pyramids with hidden edges shown. The height of the pyramid…

Rectangle With Dimensions
Rectangle with dimensions labeled. Rectangle can be used to calculate area.
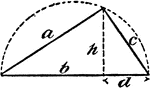
Right Triangle Inscribed In A Semicircle
An illustration of a right triangle inscribed in a semicircle.
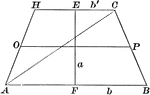
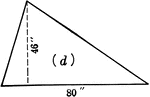
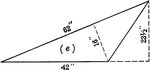
Area of a Trapezoid
Illustration of a trapezoid with altitude a and bases b and b' used to demonstrate that the area is…

Trapezoid With Dimensions
Trapezoid with dimensions labeled. Trapezoid can be used to calculate area.
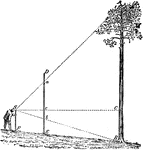
Using Proportions To Find Heights of Trees
Triangle diagram for measuring heights of trees using proportions.

Using Proportions To Find Heights of Trees
Triangle diagram for measuring heights of trees using proportions
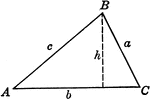
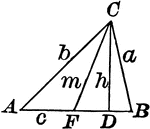
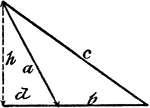
Triangle ABC With Height h
Triangle ABC with sides a,b,c labeled and angles A,B,C labeled and h labeled as height.

Triangle with Church
An illustration of a triangle comprised of a church and two lines. This illustration can be used to…
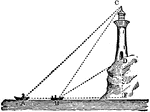
Triangle with Lighthouse
An illustration of a three triangles created with boats and a lighthouse. This is an example illustration…

Triangle with Tower
An illustration of a triangle comprised of a tower and two lines. This illustration can be used to determine…
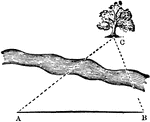
Triangle with Tree
An illustration of a triangle comprised of a tree and two lines. This is an example of a problem that…
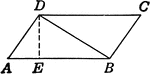
Area of Triangle
Parallelogram illustration to show where the area of a triangle formula comes from.
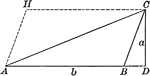
Area of a Triangle
Illustration of triangle ABC with altitude a and base b to be used to demonstrate that the area is 1/2ba.
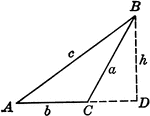
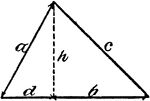
Obtuse Triangle ABC With Height h
Triangle ABC with sides a,b,c labeled and angles A,B,C labeled and h labeled as height.
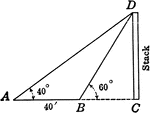
Similar Triangles for Height of Smokestack
Illustration of similar triangles used to find height of smokestack.
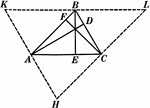
Similar Triangles With Altitudes Drawn
Illustration that shows two similar triangles with altitudes drawn.

Water Level in Multiple Connected Vessels
"When any liquid is placed in one or more of several vessels communicating with each other, it will…