Clipart tagged: ‘sin’

Adam and Eve are Punished and Cast Out of the Garden of Eden
"So he drove out the man; and he placed at the east of the garden of Eden the Cherubim, and the flame…
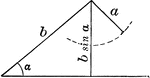
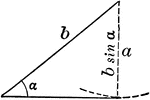
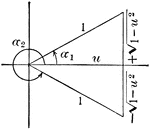
Sum of 2 Acute Angles
Illustration of two triangles, showing the sine of the sum of two acute angles expressed in terms of…

The Brazen Serpent and the Healing of the Israelites
"And Jehovah sent fiery serpents among the people, and they bit the people; and much people of Israel…
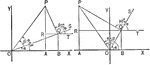
Ambiguous Case
Illustration of one possible outcome (no triangle occurs) when discussing the ambiguous case using the…
Ambiguous Case
Illustration of one possible outcome (1 triangle occurs) when discussing the ambiguous case using the…
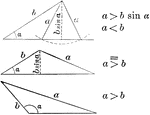
Ambiguous Case
Illustration of one possible outcome (2 triangles occur) when discussing the ambiguous case using the…

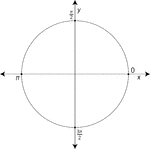
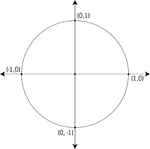
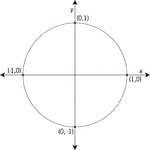
Unit Circle
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane. The…
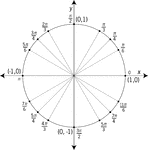
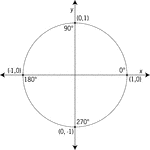
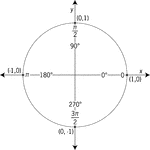
Unit Circle Labeled At Quadrantal Angles
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
Unit Circle Labeled At Special Angles
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…

Unit Circle Labeled At Special Angles
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
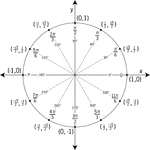
Unit Circle Labeled In 30° Increments With Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
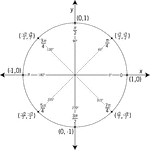
Unit Circle Labeled In 45 ° Increments
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
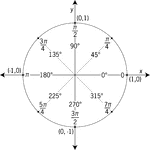
Unit Circle Labeled In 45° Increments With Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
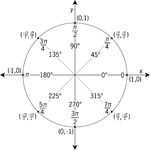
Unit Circle Labeled In 45° Increments With Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
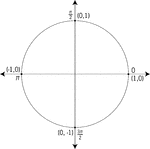
Unit Circle Labeled With Quadrantal Angles And Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane. All…
Unit Circle Labeled With Quadrantal Angles And Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
Unit Circle Labeled With Quadrantal Angles And Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
Unit Circle Labeled With Quadrantal Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane. At each…
Unit Circle Labeled With Quadrantal Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
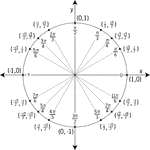
Unit Circle Labeled With Special Angles And Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
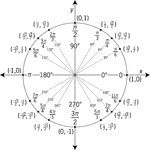
Unit Circle Labeled With Special Angles And Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
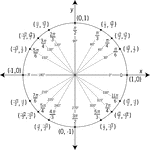
Unit Circle Labeled With Special Angles And Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
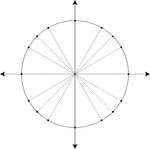
Unit Circle Marked At Special Angles
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane. All…

Jesus Carrying the Cross on the Way to Calvary
"They took Jesus therefore: and he went out, bearing the cross for himself, unto the place called The…
Angle Expressed As An Inverse Function
Illustration that can be used to show that when given an angle, expressed as an inverse function of…

Moses Breaks the Stone Tablets on Which the Ten Commandments are Written
"And it came to pass, as soon as he came nigh unto the camp, that he saw the calf and the dancing: and…

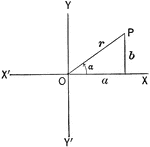
Triangles and Sectors in Quadrant I
Illustration of an angle &alpha with the vertex at the center, O, of a circle with radius OB. AC and…
Triangle in Quadrant I
Illustration of an angle &alpha with the terminal side used to draw a triangle in quadrant I.
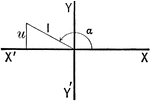
Triangle in Quadrant II
Illustration of an angle with the terminal side used to draw a triangle in quadrant II.
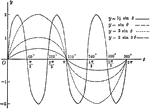
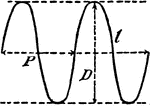
Sine Curves y= sin Ǝ, y= 1/2 sin Ǝ, y=2 sin Ǝ, y= 2 sin 3Ǝ
Sine curves of varying frequency and amplitude plotted from 0 to 2 pi. Graph of y= sin θ, y= 1/2…
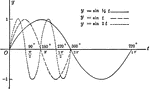
Sine Curves y= sin t, y= r sin1/2t, y= r sin 2t
Sine curves of varying frequency plotted from 0 to 2 pi. Graph of y= sin t, y= r sin1/2t, y=r sin 2t.
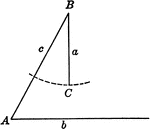
Law of Sines
Illustration two types of triangles that can be used to model the law of sines. "In a plane triangle…

Snake Giving Two Children Cake
A cartoon of a snake feeding a piece of cake to two children. A sign over the cake reads: The Forbidden…

Suovetaurilia
"The relief pictures an ancient Italian sacrifice of a bull, a ram, and a boar, offered to Mars to secure…

The Crucifixion of Jesus with Two Robbers
"And with him they crucify two robbers; one on his right hand, and one on his left." Mark 15:27 ASV…
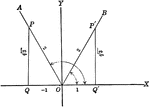
Ambiguous Case of Law of Sines Triangle
Illustration showing ambiguous case when the solution is not a triangle using law of sines.
Trigonometric Reference Triangles/Angles (60 degrees) Drawn in Quadrants
Trigonometric reference triangles/angles drawn for 60 degree reference angel in quadrants I and II.
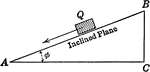
Inclined Plane Forming Right Triangle
Inclined plane forming right triangle showing the velocity of a body sliding a distance,s, down a smooth…
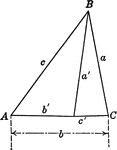
Triangles ABC and ABC'
Triangle ABC and triangle ABC'. This illustration could be used to demonstrate the law of sines.

Trigonometric Reference Triangles/Angles Drawn in Quadrants
Trigonometric reference triangles/angles drawn for reference angel in quadrants I and II. This illustration…

Jesus Tells a Crowd to Cast the First Stone
"But when they continued asking him, he lifted up himself, and said unto them, He that is without sin…

Jesus Tells a Woman to Go and Sin No More
"And they, when they heard it, went out one by one, beginning from the eldest, even unto the last: and…