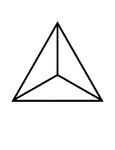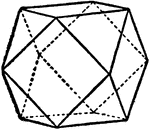
Cubo-octahedron
Represents the combination of a cube and an octahedron, with both faces being equal.
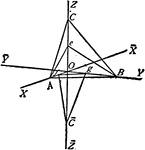
Crystallographic Axes of Reference
"...take any three edges formed by the intersection of three faces of a crystal. These axes are called…
Clinographic Drawing of a Cubic Crystal
"A drawing of a crystal showing a combination of the cube, octahedron and rhombic dodecahedron is shown,…
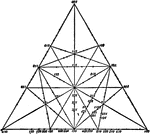
Gnomonic Projection of a Cubic Crystal
"Here the plane of projection is tangent to the sphere, and normals to all the faces are drawn fro mthe…
!["Bounded by twelve rhomb-shaped faces parallel to the six dodecahedral planes of symetry. the angles between the normals to adjacent faces are 60 degrees...[and] 90 degrees; the indices are {110}" -The Encyclopedia Britannica 1910](https://etc.usf.edu/clipart/35500/35528/rhom_35528_mth.gif)
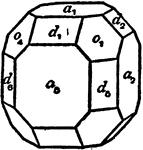
Rhombic Dodecahedron
"Bounded by twelve rhomb-shaped faces parallel to the six dodecahedral planes of symetry. the angles…

Triakis-octahedron
"This solid is bounded by twenty-four isosceles triangles, and may be considered as an octahedron with…
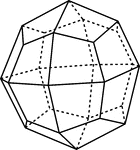
Icositetrahedron
"Bounded by twenty-four trapezoidal faces, and hence somethings called a 'trapezohedron.'" -The Encyclopedia…
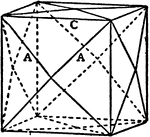
Tetrakis-hexahedron
"Like the triakis-octahedron, this solid is also bounded b twenty-four isosceles triangles, but here…
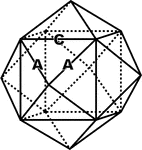
Tetrakis-hexaheron
"Like the triakis-octahedron, this solid is also bounded b twenty-four isosceles triangles, but here…
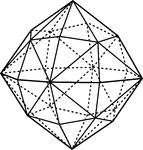
Hexakis-octahedron
"Here each face of the octahedron is replaced by six scalene triangles, so that altogether there are…
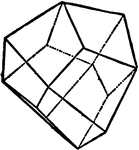
Deltoid Dodecahedron
"This is the hemihedral form of the triakis-octahedron; it has the indices {hhk} and is bounded by tweleve…
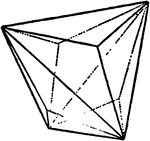
Triakis-tetrahedron
"The hemihedral form {hkk} of the icositetrahedron; it is bounded by twelve isosceles triangles arranged…
Combination of two Tetrahedra
"...a combination of these two tetrahedra, and represents a crystal of blende, in which the four larger…

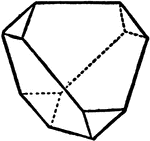
Pentagonal Dodecahedron
"This is bounded by twelve pentagonal faces, but these are not regular pentagons, and the angles over…

Dyakis-dodecahedron
"This is the hemihedral form of the hexakis-octahedron and has the indicies {hkl}; it is bounded by…
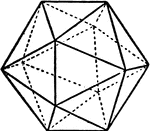
Combination of Pentagonal Dodecahedron and Octahedron
"...resembles in general appearance the regular icosahedron of geometry, but only eight f the faces…
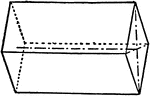
Macro-prism and Brachy-pinacoid
"This consists of four faces parallel to the brachy axis." -The Encyclopedia Britannica 1910
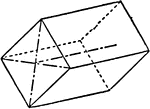
Brachy-prism and Macro-pinacoid
"This consists of four faces perpendicular to the vertical axis." -The Encyclopedia Britannica 1910
!["Here there is only a [center] of symmetry. All the forms are pina-coids, each consisting of only two paarallel faces." -The Encyclopedia Britannica 1910](https://etc.usf.edu/clipart/35500/35580/axinite_35580_mth.gif)
Crystal of Axinite
"Here there is only a [center] of symmetry. All the forms are pina-coids, each consisting of only two…
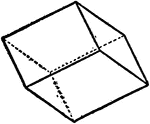
Direct Rhombohedra
"...consisting of six rhomb-shaped faces with the edges all of the equal lengths: the faces are perpendicular…
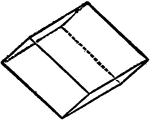
Indirect Rhombohedra
"...consisting of six rhomb-shaped faces with the edges all of the equal lengths: the faces are perpendicular…
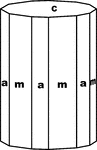
Hexagonal Prism of the First Order
"Hexagonal prism of the first order, consisting of six faces also parallel to the hexad axis, but perpendicular…
!["...is flattened parallel to one pair of faces [of the octahedron]." -The Encyclopedia Britannica 1910](https://etc.usf.edu/clipart/35600/35601/misshapen2_35601_mth.gif)
Misshapen Octahedra
"...is flattened parallel to one pair of faces [of the octahedron]." -The Encyclopedia Britannica 1910
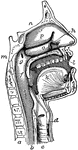
The Mouth, Nose, and Pharynx
The mouth, nose, and pharynx, with the larynx and commencement of gullet (esophagus), seen in section.…
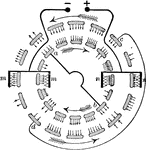
Design of the Wimhurst Machine
"The tin-foil strips or carriers on the rear plate of a Wimhurst machine are represented by the outer…

Cube
"A cube is a prism whose faces are ends are squares. All the faces of a cube are equal." —Hallock…

Prismatoid With Triangular Faces
An illustration of a prismatoid with triangular faces and points labeled.
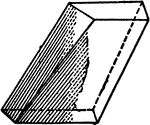
Prismatoid With Quadrilateral Faces
An illustration of a prismatoid with faces that are quadrilaterals.