Clipart tagged: ‘origin’
Origin of Eskers
Diagrams showing the origins of eskers. A) A tunnel under the ice, nearly filled with sand and gravel…
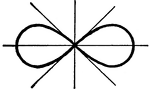
Lemniscate
A Lemniscate is, in general, a curve generated by a point moving so that the product of its distances…