Clipart tagged: ‘trapezohedron’
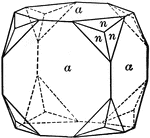
Dodecahedron, trapezohedron and hexoctahedron
"A combination of of dodecahedron, trapezohedron, and hexoctahedron." — Ford, 1912
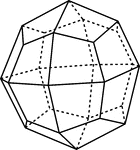
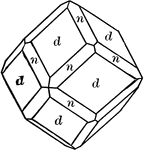
Icositetrahedron
"Bounded by twenty-four trapezoidal faces, and hence somethings called a 'trapezohedron.'" -The Encyclopedia…
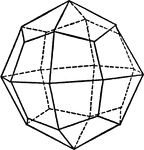
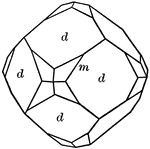
Icositetrahedron
The planes of this form are similar to trapeziums. Because it has twenty-four sides, it is usually called…
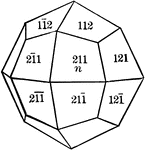
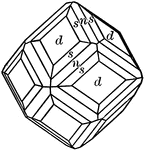
Trapezohedron
"The trapezohedron is a form composed of twenty-four trapezium-shaped faces, each of which intersects…
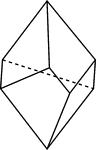
Trigonal Trapezohedron
"...bounded by six trapezoidal hedra...derivable from the scalenohedron." -The Encyclopedia Britannica…