Clipart tagged: ‘Sine’
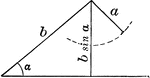
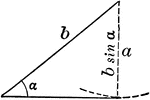
Sum of 2 Acute Angles
Illustration of two triangles, showing the sine of the sum of two acute angles expressed in terms of…
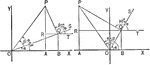
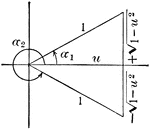
Ambiguous Case
Illustration of one possible outcome (no triangle occurs) when discussing the ambiguous case using the…
Ambiguous Case
Illustration of one possible outcome (1 triangle occurs) when discussing the ambiguous case using the…
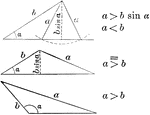
Ambiguous Case
Illustration of one possible outcome (2 triangles occur) when discussing the ambiguous case using the…

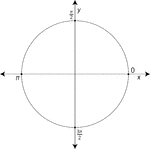
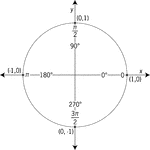
Unit Circle
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane. The…
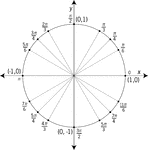
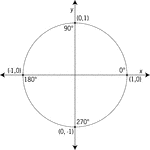
Unit Circle Labeled At Quadrantal Angles
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
Unit Circle Labeled At Special Angles
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…

Unit Circle Labeled At Special Angles
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
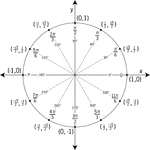
Unit Circle Labeled In 30° Increments With Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
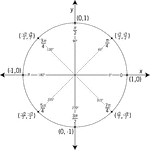
Unit Circle Labeled In 45 ° Increments
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
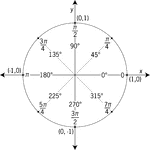
Unit Circle Labeled In 45° Increments With Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
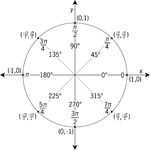
Unit Circle Labeled In 45° Increments With Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
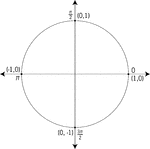
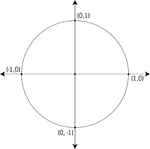
Unit Circle Labeled With Quadrantal Angles And Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane. All…
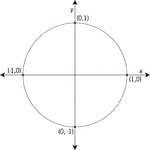
Unit Circle Labeled With Quadrantal Angles And Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
Unit Circle Labeled With Quadrantal Angles And Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
Unit Circle Labeled With Quadrantal Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane. At each…
Unit Circle Labeled With Quadrantal Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
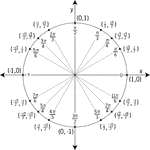
Unit Circle Labeled With Special Angles And Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
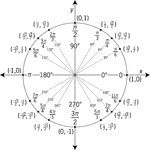
Unit Circle Labeled With Special Angles And Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
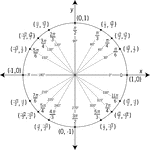
Unit Circle Labeled With Special Angles And Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
Unit Circle Marked At Special Angles
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane. All…
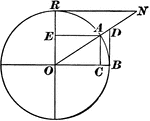
Versedsine and Coversedsine in Circle
The coversedsine is equal to 1 minus the sine. In this figure, AE is parallel to OB; hence, EO = AC…
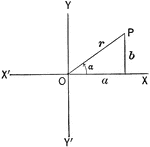
Angle Expressed As An Inverse Function
Illustration that can be used to show that when given an angle, expressed as an inverse function of…

Triangles and Sectors in Quadrant I
Illustration of an angle &alpha with the vertex at the center, O, of a circle with radius OB. AC and…
Triangle in Quadrant I
Illustration of an angle &alpha with the terminal side used to draw a triangle in quadrant I.
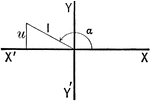
Triangle in Quadrant II
Illustration of an angle with the terminal side used to draw a triangle in quadrant II.
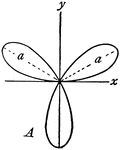
Rose
"In geometry, certain transcendental curves having, in polar coordinates, equations of the form ρ…
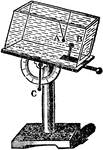
Sine Electrometer
"The sine electrometer of August, is a modification of the single pendulum electroscope, analogous in…
Law of Sines
Illustration two types of triangles that can be used to model the law of sines. "In a plane triangle…

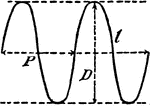
Sinusoid or Sine Wave
"The curve of sines, in which the abscissas are proportional to an angle, and the ordinates to its sine."…
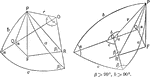
Relationships In A Spherical Triangle
Illustration used, with the law of sines, to find the relation between two sides of a spherical triangle…
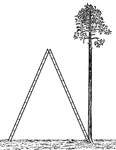
Skyscraper Giant Stepladder
Illustration of a giant stepladder, sometimes called a skyscraper stepladder, that is opened next to…
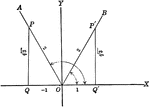
Trigonometric Reference Triangles/Angles (60 degrees) Drawn in Quadrants
Trigonometric reference triangles/angles drawn for 60 degree reference angel in quadrants I and II.

Trigonometric Reference Triangles/Angles Drawn in Quadrants
Trigonometric reference triangles/angles drawn for reference angel in quadrants I and II. This illustration…
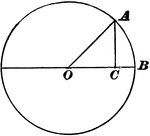
Trigonometry Triangle to Show Sine, Cosine, and Tangent
Right triangle OCA, inside of Circle O is used to show that side AC is "opposite" O and side OC is "adjacent"…