Clipart tagged: ‘analytic geometry’

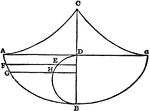
Centrodes
Aronhold stated if any three bodies have plane motion their three virtual centers are three points on…

Unit Circle
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane. The…
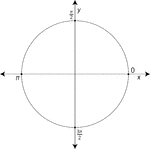
Unit Circle Labeled At Quadrantal Angles
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
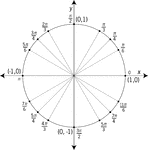
Unit Circle Labeled At Special Angles
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…

Unit Circle Labeled At Special Angles
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
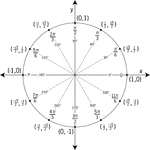
Unit Circle Labeled In 30° Increments With Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
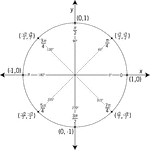
Unit Circle Labeled In 45 ° Increments
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
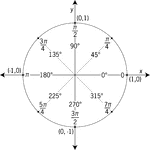
Unit Circle Labeled In 45° Increments With Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
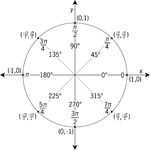
Unit Circle Labeled In 45° Increments With Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
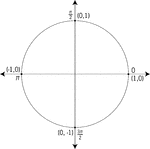
Unit Circle Labeled With Quadrantal Angles And Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane. All…
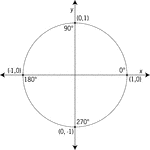
Unit Circle Labeled With Quadrantal Angles And Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
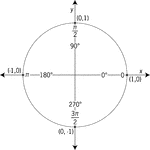
Unit Circle Labeled With Quadrantal Angles And Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
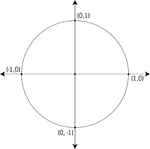
Unit Circle Labeled With Quadrantal Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane. At each…
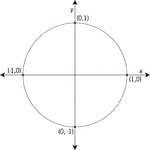
Unit Circle Labeled With Quadrantal Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
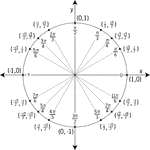
Unit Circle Labeled With Special Angles And Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
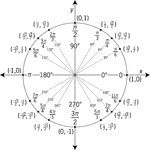
Unit Circle Labeled With Special Angles And Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
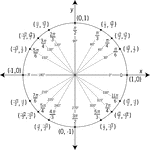
Unit Circle Labeled With Special Angles And Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
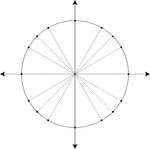
Unit Circle Marked At Special Angles
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane. All…
Geometric Inspection of Complex Numbers
Illustration showing complex numbers with a modulus equal to unity. The lines representing these numbers…
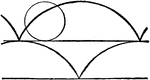
Cycloid
Illustration showing a cycloid curve. "The curve generated by a point in the plane of a circle when…
Cycloid
Illustration showing a cycloid curve. "The curve generated by a point in the plane of a circle when…
Construction Of A Cycloid
An illustration showing how to construct a cycloid. "The circumference C=3.14D. Divide the rolling circle…

Cycloids
Illustration showing cycloid curves. "The curve generated by a point in the plane of a circle when the…
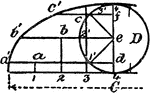
Construction Of An Ellipse Tangent To Two Parallel Lines
An illustration showing how to construct an ellipse parallel to two parallel lines A and B. "Draw a…
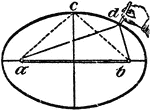
Construction Of An Ellipse
An illustration showing how to construct an ellipse. "With a as a center, draw two concentric circles…
Construction Of An Ellipse
An illustration showing how to construct an ellipse using a string. "Having given the two axes, set…
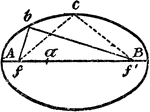
Construction Of An Ellipse
An illustration showing how to construct an ellipse using circle arcs. "Divide the long axis into three…
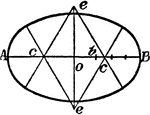
Construction Of An Ellipse
An illustration showing how to construct an ellipse using circle arcs. "Given the two axes, set off…
Construction Of An Ellipse
An illustration showing how to construct an ellipse. Given the two axes, set off half the long axis…

Construction Of An Evolute Of A Circle
An illustration showing how to construct an evolute of a circle. "Given the pitch p, the angle v, and…
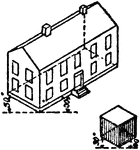
Construction Using Isometric Perspective
An illustration showing how to use isometric perspective. "This kind of perspective admits of scale…
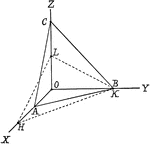
Plane
Illustration showing a how in "analytic geometry it is customary to specify the position of a plane…
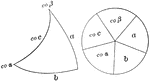
Napier's Right Spherical Triangle
Illustration of a right spherical triangle and the five circular parts placed in the sectors of a circle…
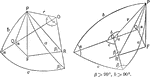
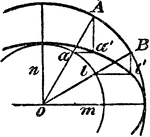
Relationships In A Spherical Triangle
Illustration used, with the law of sines, to find the relation between two sides of a spherical triangle…
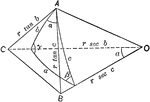
Relationships In A Spherical Triangle
Illustration used, with the law of cosines, to find the relation between the three sides and an angle…
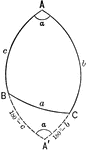
Relationships In A Spherical Triangle
Illustration used to extend the law of cosines when finding the relation between the three sides and…
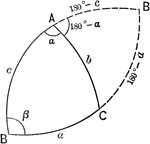
Relationships In A Spherical Triangle
Illustration used to extend the law of cosines when finding the relation between the three sides and…

Right Spherical Triangle
Illustration of a right spherical triangle with a and b the sides, and α and β the angles…
Archimedean Spiral
Illustration of a spiral named after the 3rd century BC Greek mathematician Archimedes.
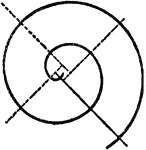
Construction Of A Spiral
An illustration showing how to construct a spiral with compasses and four centers. "Given the pitch…
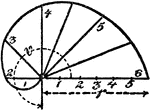
Construction Of An Arithmetic Spiral
An illustration showing how to construct an arithmetic spiral. "Given the pitch p and angle v, divide…
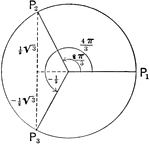
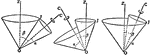
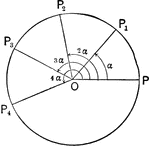
Cubed Roots of Unity
Illustration showing how to find the cubed roots of unity by applying DeMoivre's Theorem.

Fifth Roots of Unity
Illustration showing how to find the fifth roots of unity by applying DeMoivre's Theorem.