Clipart tagged: ‘dodecahedron’
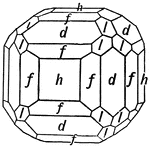
Amalgam
This form shows the cube (h), the dodecahedron (d), the tetrahexahedron (f), and the icositetrahedron…
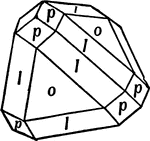
Beveled Tetrahedron
This form shows a tetrahedron (o) with its edges beveled by the trigonal tristetrahedron (l), and its…
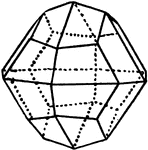
Combination of Pentagonal Dodecahedron and Cube
Represents a combination of a pentagonal dodecahedron and cube, and are common in pyrites.
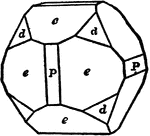
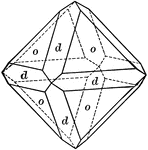
Combination of Pentagonal Dodecahedron, Cube and Octahedron
Represents the combination of pentagonal dodecahedron, cube, and octahedron.
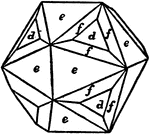
Combination of Pentagonal Dodecahedron, Dyakis-dodecahedron, and Octahedron
Represents the combination of pentagonal dodcahedron, dyakis-dodecahedron and octahedron.
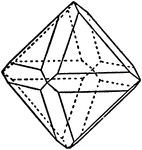
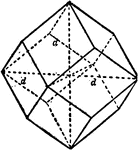
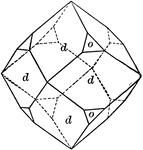
Combination of Rhombic Dodecahedron and Octahedron
"...shows the rhombic dodecahedron in combination with the octahedron." -The Encyclopedia Britannica…
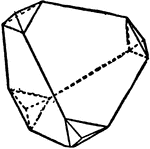
Combination of Tetrahedron and Rhombic Dodecahedron
A combination of a tetrahedron and a rhombic dodecahedron.
Cube, dodecahedron and tetrahedron
"A combination of cube, dodecahedron, and tetrahedron." — Ford, 1912
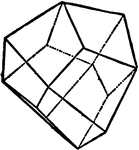
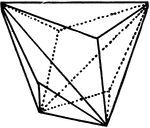
Deltoid Dodecahedron
"This is the hemihedral form of the triakis-octahedron; it has the indices {hhk} and is bounded by tweleve…
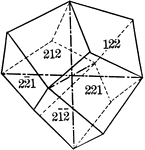
Deltoid dodecahedron
"The faces of the deltoid dodecahedron correspond to one-half those of the trisoctahedron." —…

Great Dodecahedron
A regular solid each face of which has the same boundaries as five covertical faces of an ordinary icosahedron.

Pattern for Dodecahedron
Pattern that can be cut out and folded to construct a regular dodecahedron. Fold on the dotted lines,…
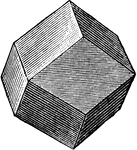
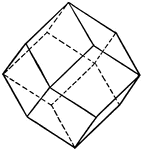
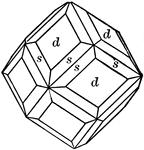
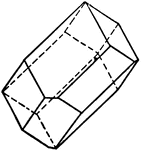
Rhombic Dodecahedron
A solid consisting of 12 similiar faces, each of which is rhomb, the angle between any two adjacent…

Stellated Dodecahedron
A regular solid each face of which formed by stellating a face of the dodecahedron.
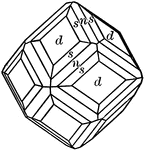
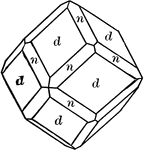
Dodecahedron, trapezohedron and hexoctahedron
"A combination of of dodecahedron, trapezohedron, and hexoctahedron." — Ford, 1912
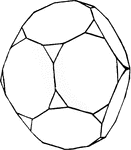
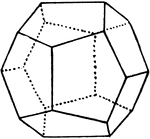
Truncated Dodecahedron
A regular dyocaetriacontahedron formed by cutting off the faces of a regular dodecahedron parallel to…

Dyakis-dodecahedron
"This is the hemihedral form of the hexakis-octahedron and has the indicies {hkl}; it is bounded by…
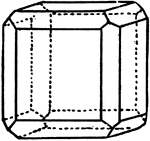
Hexahedron and Dodecahedron
Illustration showing the combination of a hexahedron and an dodecahedron.
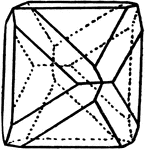
Octahedron and Dodecahedron
Illustration showing the combination of a octahedron and an dodecahedron.

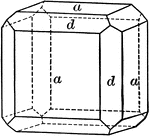
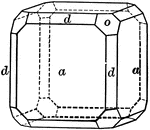
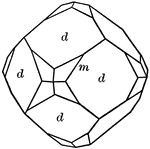
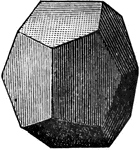
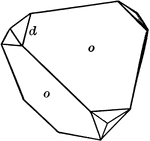
Pentagonal Dodecahedron
"This is bounded by twelve pentagonal faces, but these are not regular pentagons, and the angles over…
!["At the freezing point [phosphorus] hardens, becomes brittle, and shows, on being broken, evidences of crystalline structure, the crystals being dodecahedral." —Hallock 1905](https://etc.usf.edu/clipart/36100/36184/phosphorus_36184_mth.gif)
Phosphorus
"At the freezing point [phosphorus] hardens, becomes brittle, and shows, on being broken, evidences…

Regular Polyhedrons
Illustration of regular polyhedrons: tetrahedron, hexahedron, octahedron, dodecahedron, icosahedron.
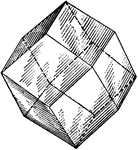
Rhombic Dodecahedron
"Science has succeeded in classifying the thousands of known crystals in six systems, to each of which…
!["Bounded by twelve rhomb-shaped faces parallel to the six dodecahedral planes of symetry. the angles between the normals to adjacent faces are 60 degrees...[and] 90 degrees; the indices are {110}" -The Encyclopedia Britannica 1910](https://etc.usf.edu/clipart/35500/35528/rhom_35528_mth.gif)
Rhombic Dodecahedron
"Bounded by twelve rhomb-shaped faces parallel to the six dodecahedral planes of symetry. the angles…

Various Solid Forms
Illustration containing a tetrahedron, hexahedron, octahedron, dodecahedron, and icosahedron, placed…
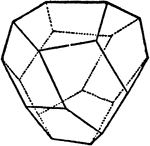
Tetrahedral Pentagonal Dodecahedron
"This is bounded by twelve irregular pentagons, and is a tetartohedral or quarter-faced for of the hexakis-octahedron."…
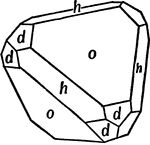
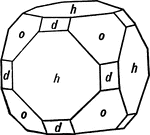
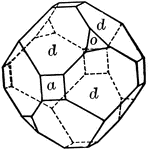
Tetrahedron, Cube, and Dodecahedron in Combination
This form shows a tetrahedron (o), cube (h), and dodecahedron (d) in combination.