The Miscellaneous Solid Forms ClipArt gallery offers 93 images of uncommon 3-dimensional figures including hexahedrons, diploids, tetrahexahedrons, and more.
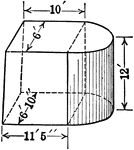
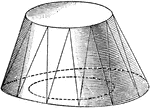
Composite Figure of Quadrilateral Frustum With Half of a Cylinder Attached
An illustration of a composite figure made up of a quadrilateral frustum and half of a cylinder. Frustum…
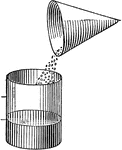
Comparative Volumes Of A Cone And Cylinder
Illustration used to compare the volumes of a cone and a cylinder by emptying sand from the cone into…

Comparative Volumes Of A Cone, Sphere, And Cylinder
Illustration used to compare the volumes of a cone, a sphere, and a cylinder.

Cube with Additions 1
A cube (A) has sides of 20 inches in length each, making its solid contents equal 8000 cubic inches.…

Cube with Additions 2
In order to fill in the spaces from the three 2000 cubic inch additions, four new additions must be…

Cube with Additions 3
This is the final form of the original 20x20x20 inch or 8000 cubic inch cube with the addition of 7625…
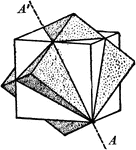
Twinned cubes
"A penetration twin, since the two individuals interpenetrate each other." — Ford, 1912
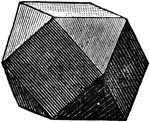
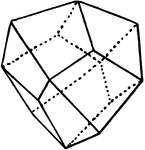
Cuboctahedron
A solid with fourteen faces formed by cutting off the corners of a cube parallel to the coxial octahedron…

Comparative Surfaces Of A Cylinder And Sphere
Illustration used to compare the surfaces of a cylinder and a sphere.
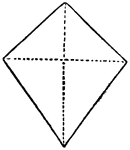
Deltoid
"A four-sided figure, formed of 2 unequal isosceles triangles on different sides of a common base."…
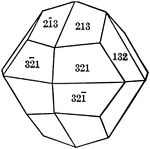
Diploid
"The diploid is a rare form found only in this class. It is composed of twenty-four faces which correspond…
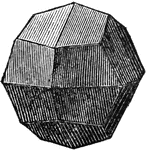
Diploid
A solid belonging to the isometric system, with 24 trapezoidal planes. It is the parallel hemihedral…
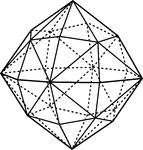
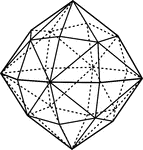
Hexakis-octahedron
"Here each face of the octahedron is replaced by six scalene triangles, so that altogether there are…
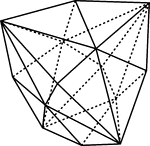
Hexakis-tetrahedron
"The hemihedral form {hkl} of the hexakis-octahedron; it is bounded by twenty-four scalene triangles…
Hexakistetrahedron
"The faces of the hexakistetrahedron correspond to one-half the faces of the hexoctahedron." —…
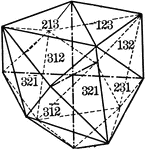
Hexoctahedron
"The hexoctahedron is a form composed of forty-eight triangular faces, each of which cuts differently…
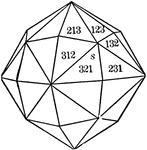
Hexoctahedron
This form is bounded by forty-eight similar scalene triangles. Its solid angles are of three kinds:…
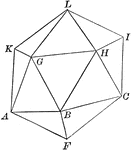
Part of an Icosahedron
Illustration of the bottom part of an icosahedron. The base consists of a regular pyramid, upon which…
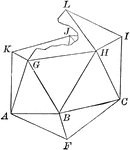
Partial Construction of an Icosahedron
Illustration of the steps to a construction of an icosahedron. The base consists of a regular pyramid,…
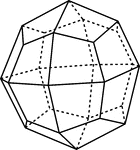
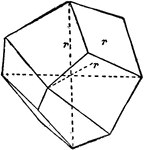
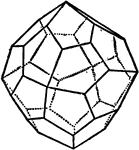
Icositetrahedron
"Bounded by twenty-four trapezoidal faces, and hence somethings called a 'trapezohedron.'" -The Encyclopedia…
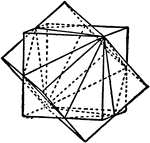
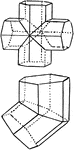
Interpenetrating Twinned Cubes
"Here one cube may be brought into the position of the other by a rotation of 180 degrees about a traid…
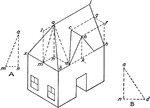
Practical Projection Of An Irregular Solid
Illustration showing a general way the method of arranging the triangles on the irregular surface of…
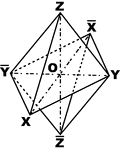
Monoclinic Axes and Hemi-pyramid
"Prisims with edges parallel to neither of the axes OX and OY...are usually called hemi-pyramids." -The…
Twinned octahedron
"A contact twin, since the two individuals lie simply in contact with each other upon a certain plane."…
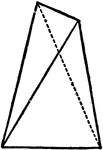
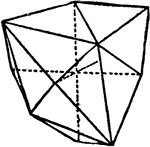
Orthorhombic Bisphenoid
"general form...bounded by four scalene triangles." -The Encyclopedia Britannica 1910
Pentagonal Icositetrahedron
"This is the only simple form in this class which differs geometricalled from those of the holosymmetric…
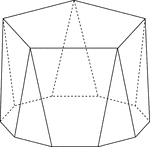
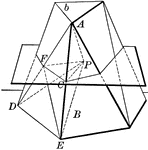
Polyhedron With Pentagon Bases
Illustration of a pentagonal polyhedron that is formed by having two parallel congruent pentagonal bases…

Polyhedron With Pentagon Bases
Illustration of a pentagonal polyhedron that is formed by having two parallel congruent pentagonal bases…
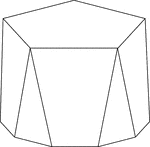
Polyhedron With Pentagon Bases
Illustration of a pentagonal polyhedron that is formed by having two parallel congruent pentagonal bases…

Regular Polyhedrons
Illustration of regular polyhedrons: tetrahedron, hexahedron, octahedron, dodecahedron, icosahedron.
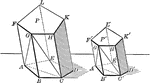
Similar Polyhedrons
Two similar polyhedrons may be decomposed into the same number of tetrahedrons similar, each to each,…
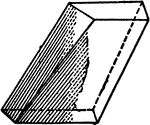
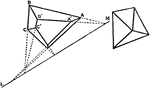
Prismatoid With Quadrilateral Faces
An illustration of a prismatoid with faces that are quadrilaterals.

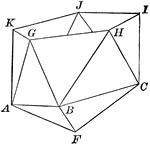
Prismatoid With Triangular Faces
An illustration of a prismatoid with triangular faces and points labeled.
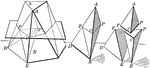
Prismatoid Illustration for Volume
Illustration to show how volume of a prismatoid is found. "The volume of a prismatoid is equal to the…
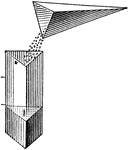
Comparative Volumes Of A Pyramid And Prism
Illustration used to compare the volumes of a pyramid and a prism by emptying sand from the pyramid…