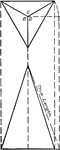The Pyramids ClipArt gallery offers 76 examples of solid geometric figures with a base that is a polygon and sides that are triangular in shape and meet at a common point at the top, known as the apex.
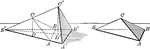
Triangular Pyramids for Volume
Illustration showing that the volume of 2 triangular pyramids, having the same trihedral angle of the…

Development of Rectangular Pyramid
The illustration of a rectangular pyramid unfolded by creating edges equal length to the base and meeting…
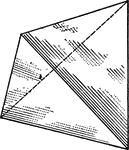
Regular Tetrahedron
"Science has succeeded in classifying the thousands of known crystals in six systems, to each of which…
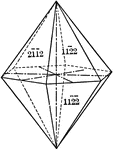
Pyramid of the second order
"This is a form composed of twelve isoceles triangular faces, each of which intersects two of the horizontal…
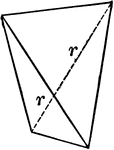
Sphenoid
"It consists of four isoceles triangular faces which intersect all three of the crystallographic axes,…

Sphenoid
"It consists of four isoceles triangular faces which intersect all three of the crystallographic axes,…
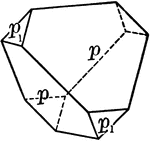
Sphenoid, positive and negative
"It consists of four isoceles triangular faces which intersect all three of the crystallographic axes,…
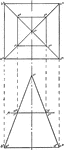
Intersection of Square Pyramid and a Plane
Illustration of the intersection of a square pyramid and a plane.
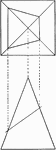
Intersection of Square Pyramid and a Plane
Illustration of the intersection of a square pyramid and a plane.
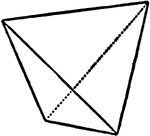
Tetrahedron
"This is bounded by four equilateral triangles and is identical with the regular tetrahedron of geometry."…

Negative tetrahedron
"The tetrahedron is a form composed of four equilateral triangular faces, each of which intersects all…

Positive tetrahedron
"The tetrahedron is a form composed of four equilateral triangular faces, each of which intersects all…
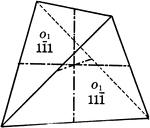
Positive and negative tetrahedrons
"If a positive and negative tetrahedron occured together with equal development, the resulting crystal…

Intersection of Triangular Pyramid and a Plane
Illustration of the intersection of a triangular pyramid and a plane.