This mathematics ClipArt gallery offers 213 illustrations of common geometric constructions. Geometric constructions are made with only the use of a compass and a straight edge. In addition to the constructions of different types of polygons, images include those used to show how to bisect a line, angle, and arc.
Construction of Dividing Lines
A line which is divided into equal parts, shown by construction and square.
Construction of an Equal Angle Given a Point and a Straight Line
Illustration of the construction used to create an equal angle given a point in a given straight line…
Construction of Escribed Circles With Ex-centres
Illustration of the construction used to escribe circles with centres (centers) called ex-centres of…
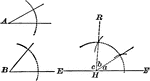
Construction to Find the Third Angle of a Triangle When Given Two Angles
Illustration of the construction used to find the third angle of a triangle when two of the angles are…
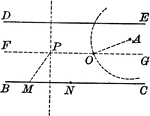
Construction of a Circle Through a Given Point that Cuts Chords of Given Lengths From Parallels
Illustration used to construct a circle that shall pass through a given point and cut chords of a given…
Construction to Inscribe a Circle in a Triangle
Illustration of the construction used to inscribe a circle in a given triangle.
Construction of a Parallelogram When Given Two Sides and Included Angle
Illustration of the construction used to make a parallelogram when given two sides and the included…
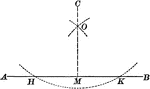
Construction of Perpendicular Upon a Given Line From an External Point
Illustration to let fall a perpendicular upon a given line from a given external point.
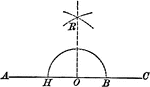
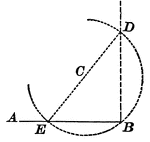
Construction of Perpendicular From a Given Point on a Straight Line
Illustration of the construction of a perpendicular to a line when given a point O on the straight line.
Construction of Perpendicular From a Given Point on a Straight Line
Illustration of the construction of a perpendicular to a line when given a point B on the straight line.
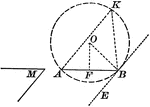
Construction to Describe a Segment of a Circle in Which an Angle Can Be Inscribed
Illustration of the construction used upon a given straight line, to describe a segment of a circle…
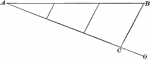
Construction of a Straight Line Divided Into Equal Parts
Illustration of the construction used to divide a straight line into a given number of equal parts.

Construction of a Straight Line Parallel to a Given Straight Line
Illustration of the construction used to create straight line parallel to a given straight line through…
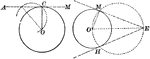
Construction of Tangent Line Through a Given Point to a Given Circle
Illustration of the construction used to draw a tangent to a given circle through a given point.
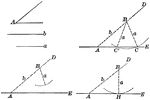
Construction of a Triangle When Given Two Sides and the Angle Opposite (Ambiguous Case)
Illustration of the construction used to make a triangle when given two sides and the angle opposite…
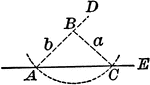
Construction of a Triangle When Given Two Sides and the Angle Opposite (Ambiguous Case)
Illustration of the construction used to make a triangle when given two sides and the angle opposite…

Construction of a Triangle When Given Two Sides and the Angle Opposite (Ambiguous Case)
Illustration of the construction used to make a triangle when given two sides and the angle opposite…
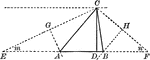
Construction of a Triangle Given Perimeter, Angle, Altitude
Illustration used to construct a triangle , given the perimeter, one angle, and the altitude from the…
Construction of a Triangle When Given a Side and Two Angles
Illustration of the construction used to make a triangle when given a side and two angles.
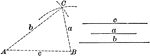
Construction of a Triangle When Given Three Sides
Illustration of the construction used to make a triangle when given three sides.
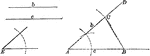
Construction of a Triangle When Given Two Sides and Included Angle
Illustration of the construction used to make a triangle when given two sides and the included angle.
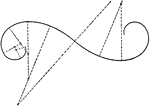
Curve Inked with Circle Arcs
"Any noncircular curve may be approximated by tangent circle arcs, selecting a center by trial, drawing…
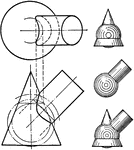
Intersection of Cylinder and Cone
An illustration of finding an intersection of a cone and cylinder by either cutting the vertex of the…
Cycloid
"A cycloid is the curve generated by the motion of a point on the circumference of a circle rolled along…
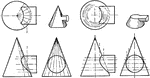
Intersection of Cylinder and Cone
An illustration of finding an intersection of a cone and cylinder by either cutting the vertex of the…
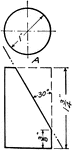
Development Exercise of Cylinder
An exercise problem in creating a development or rolled out surface of a cylinder in a 4" by 5" drawing…
Construction Of A Cyma
An illustration showing how to construct a cyma, or two circle arcs that will tangent themselves, and…
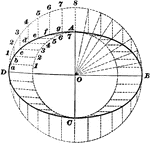
Determining Points on Ellipse Using Circles
Using C as a center, draw two circles with different diameters. The intersection of the diameter lines…
Development of Cone
A development, or rolled out, cone where the point A is the meeting point for the sides. The development…
Development of Cylinder
A rolled out, or development, of the cylinder. The development is created by drawing the top curve with…
Development of Rectangle Pyramid
The development, or unfolded prism, of the rectangular pyramid. The sides of the prism is joined at…
Development of Triangle Pyramid
A development, or rolled out, triangle pyramid. The image is created by making an arc at the bottom…
Development of Two Intersecting Cylinder
A development, or rolled out image, of two cylinders intersecting each other. The large rectangular…

Construction Used to Divide a Line Into Equal Parts
Illustration used to show how to divide a line into any number of equal parts by construction.
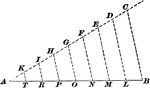
Construction Of Dividing A Line
Illustration used to show how to divide a given straight line into required number of equal parts.
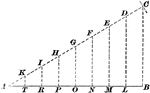
Construction Of Dividing A Line
Illustration used to show how to divide a given straight line into required number of equal parts.
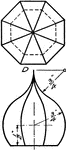
Development Exercise of Dome and True Shape of Hip
A development or rolled out image exercise problem of the dome and finding the true shape of the hip,…

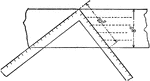
Drawing Maltese Cross using T-square, Spacers, and Triangles
"Draw three-inch square and one-inch square. From the corners of inner square draw lines to outer square…
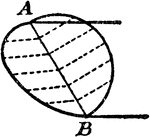
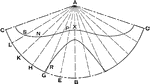
Construction Of An Ellipse Tangent To Two Parallel Lines
An illustration showing how to construct an ellipse parallel to two parallel lines A and B. "Draw a…

Epicycloid and Hypocycloid
Epicycloid is generated by a circle rolled outside of another circle, whereas a hypocycloid is circle…
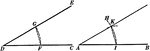
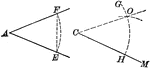
Construction Of An Equal Angle
Illustration used to show how to construct an angle equal to a given angle when given a vertex and a…
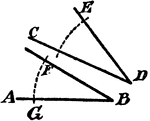
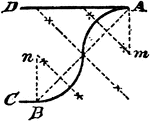
Construction Of An Equal Angle
An illustration showing the construction used to erect an equal angle. "With D as a center, draw the…
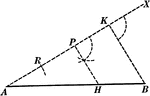
Line Divided Into Equal Parts
Illustration used to show how to divide a given straight line into any number of equal parts.

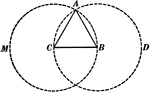
Construction Of An Equilateral Triangle Inscribed In A Circle
An illustration showing how to construct an equilateral triangle inscribed in a circle. "With the radius…
Construction Of Equilateral Triangle
Illustration used to show how to construct an equilateral triangle, with a given line as a side.
Construction Of Equilateral Triangle
Illustration used to show how to draw an equilateral triangle when given one side.
Construction Of Equilateral Triangle
Illustration used to show how to draw an equilateral triangle when given the altitude.
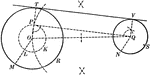
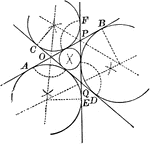
Construction of an External Tangent to 2 Circles
Illustration used to show how "to construct a common external tangent to two given circles."
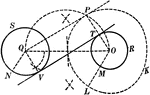
Construction of an 2 External Tangents to 2 Circles
Illustration used to show how to construct two common external tangents to two given circles.
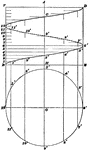
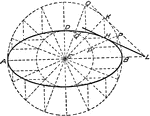
Construction Of Helix
Illustration used to show how to draw a helix when the pitch and the diameter are given.
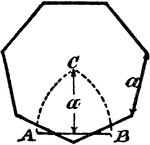
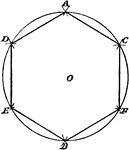
Construction Of A Heptagon
An illustration showing how to construct a heptagon, or septagon. "The appotem a in a hexagon is the…
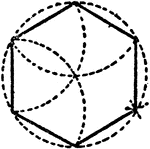
Construction Of A Hexagon In A Circle
An illustration showing how to construct a hexagon in a given circle. "The radius of the circle is equal…
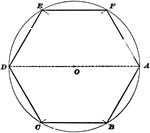
Construction Of Hexagon Inscribed In Circle
Illustration used to show how to inscribe a regular hexagon in a given circle.
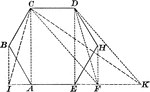
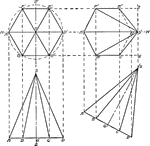
Hexagon Used to Construct Equivalent Triangle
Illustration of a how to construct a triangle equivalent to a given hexagon/polygon.
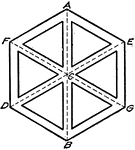
Drawing Hexagonal Figure
"Through the center of the space draw the three construction lines, AB vertical, DE and FG at 30 degrees.…