Clipart tagged: ‘bar’
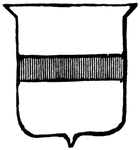
Shield Showing Bar
Argent, two closets, azure. The closet is a diminutive of the bar, and is half its width. -Hall, 1862
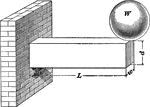
Cantilever
"A cantilever is a beam, bar, rod, etc., fixed at one end and subjected to a transverse stress. It has…

Cantilever
"When the load is uniformly distributed on a cantilever of any cross-section, it will sustain a load…
Center of Inertia
"But, suppose the same bar or iron, whose inertia was overcome by raising the centre, to have balls…

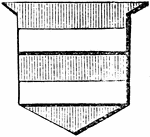
Shield Showing Closet
Gules, two barrulets, argent. The barrulet is half the width of the closet. -Hall, 1862

Closets
"Or, two closets azure. CLOSET. A diminutive of the bar, being only one half its width." -Hall, 1862

William M. Evarts
"Both as a lawyer and a statesman Mr. Evarts ranks high." —The Popular Cyclopedia, 1888
Rail Fork
"A track-layers' bar having two parallel blunt arms at the end the space between which is designed to…
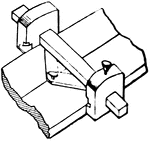
Bisecting Gauge
"Bisecting gage, a gage formed by a bar carrying two heads or cheeks connected by two arms of equal…
Conventional Breaks Symbols of Pipe or Tubing by Cutting Diameter
The conventional break symbol for drawing a pipe or tubing by cutting the diameter in half.

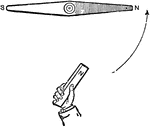
Dipping needle
"A small bar magnet suspended in such a manner as to allow it to assume its chosen position relative…
Conventional Breaks Symbols of Pipe or Tubing without Cutting Diameter
A shortcut drawing pipe or tubing conventional break to draw a pipes and tubes by shortening the length…

Magnetic polse
The outline of a bar magnet, and the influence of its poles on a surface covered with iron filings.

Seal Press
"A press or stamp bearing dies on its jaws, or a die and a bed, for imprinting or embossing any device…
Conventional Breaks Symbols of Round Section Cylinder
A conventional break symbol for a round section to use as a shortcut in shortening the length of the…
Screw Stock
"A handle for holding the threaded die by which the thread is cut on a bar, a nut, or a pipe; a die-stock;…

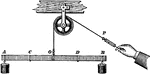
Simple Lever
"Any rod, or bar, which is used in raising a weight, or surmounting a resistance, by being placed on…

Demonstration of Static Electricity
A hand with bar demonstrating the attractive properties of static electricity.
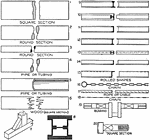
Conventional Breaks and Other Symbols
A series of illustration with conventional breaks and other symbols. The break in the bar is used as…
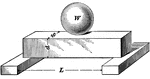
!["[This illustration] shows a third form of the wheel and axle. Here the axle A is vertical, instead of horizontal. A bar inserted in its head, at the extremity of which the hand is applied, takes the place of the wheel." —Quackenbos 1859](https://etc.usf.edu/clipart/36300/36346/vert_whax_36346_mth.gif)
Vertical Wheel and Axle
"[This illustration] shows a third form of the wheel and axle. Here the axle A is vertical, instead…