Clipart tagged: ‘figure’
Bracelet
This bracelet is in the form of leaves and flowers. In the center are winged figures that are supporting…
Wall Bracket
This wall bracket is ornamented with a female figure in the center, surrounded by foliage.
Bronze Figure
"Bronze figure, originally applied a relief. Found at Tarentum. Apparently in the style of Lysippus."…

Brooch
This brooch is designed in a Renaissance style with a figure in the center and a bird on each side.

Cabinet
This cabinet is carved using English walnut wood in an Italian style. It is richly ornamented with an…

Antique Candelabrum Capital
The Antique candelabrum capital has a plate or cup like form on the top where a lamp or candle can be…
Greek Caryatid
The Greek Caryatid is a female figure used as a support in place of a column. It is found in the temple…

Modern Caryatid
The modern caryatid is two female figures side by side used as supports in place of columns.

Modern Caryatid
The modern caryatid is two female figures side by side used as supports in place of columns.

Modern Caryatid
The modern caryatid is two female figures side by side used as supports in place of columns.
Modern Caryatid
The modern caryatid is two female figures side by side used as supports in place of columns.
Modern Caryatid
The modern caryatid is two female figures side by side used as supports in place of columns.
Renaissance Console
This Renaissance console is shown in its side view. It is richly ornamented with spiral curved leaves…

Female Doll Figure
A doll is an object that represents a baby or other human being. Dolls have been around since the dawn…

Figurehead of Ship
"An ornamental figure, as a statue or bust, on the projecting part of the head of a ship, over the cutwater…

Proportions of human figure
"The proportions of the human figure. As handed down to us by Vitruvius and described by Joseph Bonomi."…

Book Cover Ornament
This book cover ornament is used as a decorative piece placed on the corner of a book cover. The ornament…

Cornice Pole-End
This cornice pole-end is a British design in a floral style. It has a figure and bunches of hops in…

Right Rectangular Prism
Illustration of a right rectangular prism with the height greater than the length and width. The bases…
Right Rectangular Prism
Illustration of a right rectangular prism. The bases are congruent rectangles and the opposite faces…
Right Rectangular Prism
Illustration of a right rectangular prism that is viewed at an angle. The bases are congruent rectangles…
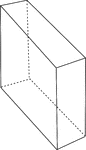
Right Rectangular Prism
Illustration of a right rectangular prism that is viewed at an angle. The bases are congruent rectangles…
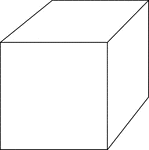
Right Rectangular Prism
Illustration of a right rectangular prism. The bases are congruent rectangles and the opposite faces…

Right Rectangular Prism
Illustration of a right rectangular prism with the height greater than the length and width. The bases…
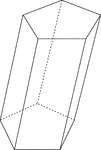
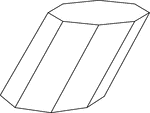
Skewed Pentagonal Prism
Illustration of a skewed pentagonal prism. The prism is non-right. The hidden edges are shown.
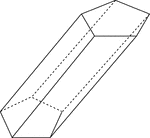
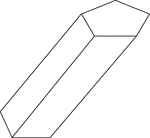
Skewed Pentagonal Prism
Illustration of a skewed pentagonal prism. The prism is non-right. The hidden edges are shown.
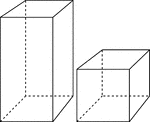
2 Rectangular Prisms
Illustration of 2 right rectangular prisms. The bases are congruent, but the height of the smaller prism…
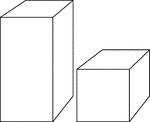
2 Rectangular Prisms
Illustration of 2 right rectangular prisms. The bases are congruent, but the height of the smaller prism…
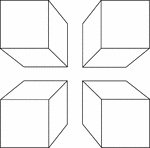
4 Congruent Rectangular Prisms
Illustration of 4 congruent rectangular prisms placed in the shape of a square. They are arranged to…

Sculpture
This sculpture depicts two mermaids at the base, a small figure in the center and a lion holding a shield…
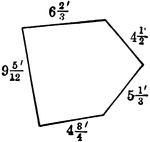
Pentagon With Sides Labeled
Illustration of a pentagon with sides measuring 6 2/3', 4 1/2', 5 1/3', 4 3/4', and 9 5/12'.
Ice Spoon
This ice spoon is used to assist the ice tongs in removing carrying ice. The handle terminates with…
Mask Terminus
The mask terminus is a modern design that is found on a chimney. It is ornamented with festoons and…

Vase
This vase is an antique design, Greek or Roman. It has two handles and a design of a figure in the center…