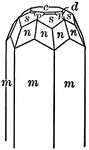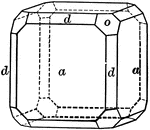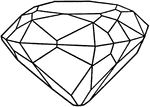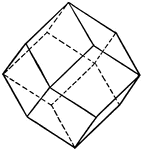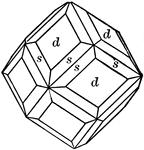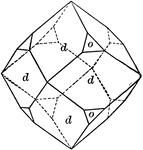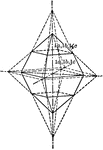
Sulphur crystal
"The forms present upon it are two pyramids of different slope but each intersecting all three of the…
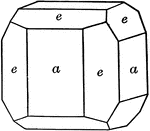
Cube and pyritohedron
"A combination of cube and pyritohedron, in which it will be noted that the faces of the pyritohedron…

Cube and tetrahedron
"A combination of cube and tetrahedron. It will be noted that the tetrahedron faces truncate the alternate…
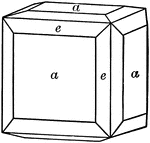
Cube and tetrahexahedron
"A cube with its edges beveled by the faces of a tetrahexahedron." — Ford, 1912

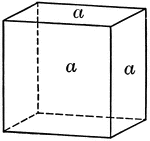
Cube with Additions 1
A cube (A) has sides of 20 inches in length each, making its solid contents equal 8000 cubic inches.…

Cube with Additions 2
In order to fill in the spaces from the three 2000 cubic inch additions, four new additions must be…

Cube with Additions 3
This is the final form of the original 20x20x20 inch or 8000 cubic inch cube with the addition of 7625…
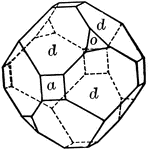
Cube, dodecahedron and tetrahedron
"A combination of cube, dodecahedron, and tetrahedron." — Ford, 1912
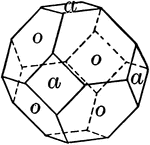
Octahedron trunctuated by cube
"When a corner or an edge of one form is replaced by a face of another form, the first is said to be…
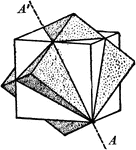
Twinned cubes
"A penetration twin, since the two individuals interpenetrate each other." — Ford, 1912

Cup
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
Cup
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…

Cup
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
Cup
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
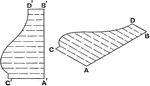
Drawing Irregular Isometric Curves of Solid
The illustration of an irregular curves for solid. The isometric projection of the curve can be drawn…
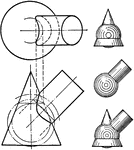
Intersection of Cylinder and Cone
An illustration of finding an intersection of a cone and cylinder by either cutting the vertex of the…
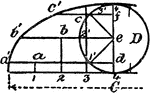
Construction Of A Cycloid
An illustration showing how to construct a cycloid. "The circumference C=3.14D. Divide the rolling circle…

Cylinder
A cylinder is a body of uniform diameter throughout its entire length, whose ends are equal parallel…

Cylinder
A body of roller-like form, of which the longitudinal section is oblong, and the cross-section is circular.
Intersection of Cylinder and Cone
An illustration of finding an intersection of a cone and cylinder by either cutting the vertex of the…
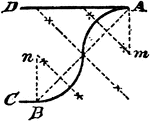
Construction Of A Cyma
An illustration showing how to construct a cyma, or two circle arcs that will tangent themselves, and…

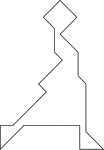
Dancer
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
Dancer
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…

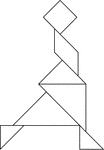
Dancer
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
Dancer
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…

Datolite
"Monoclinic. Habit varied. Crystals usually nearly equidimensional in the three axial directions and…
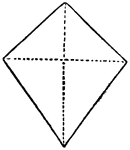
Deltoid
"A four-sided figure, formed of 2 unequal isosceles triangles on different sides of a common base."…
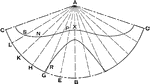
Development of Cone
A development, or rolled out, cone where the point A is the meeting point for the sides. The development…
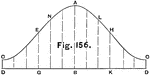
Development of Cylinder
A rolled out, or development, of the cylinder. The development is created by drawing the top curve with…
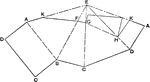
Development of Rectangle Pyramid
The development, or unfolded prism, of the rectangular pyramid. The sides of the prism is joined at…
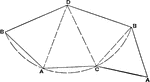
Development of Triangle Pyramid
A development, or rolled out, triangle pyramid. The image is created by making an arc at the bottom…
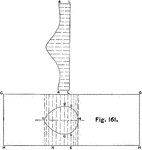
Development of Two Intersecting Cylinder
A development, or rolled out image, of two cylinders intersecting each other. The large rectangular…
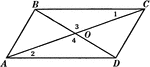
Parallelogram With Diagonals
Illustration of a parallelogram with diagonals AC and BD intersecting at point O.
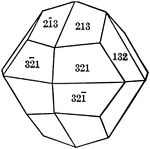
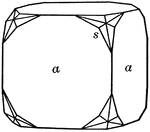
Diploid
"The diploid is a rare form found only in this class. It is composed of twenty-four faces which correspond…
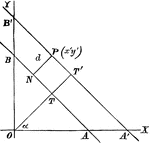
Perpendicular Distance
Finding the perpendicular distance of points whose equation is x cosa + y sina = p.

Diver
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
Diver
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…

Diver
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
Diver
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
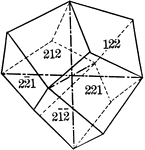
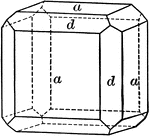
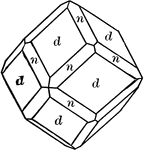
Deltoid dodecahedron
"The faces of the deltoid dodecahedron correspond to one-half those of the trisoctahedron." —…
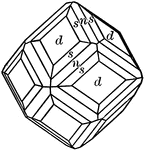
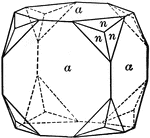
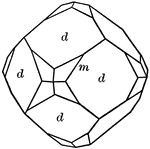
Dodecahedron, trapezohedron and hexoctahedron
"A combination of of dodecahedron, trapezohedron, and hexoctahedron." — Ford, 1912