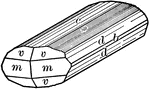
Chalcocite
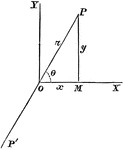
"Orthorhombic. Usually in small tabular crystals with hexagonal outline. Striated parallel to the brachy-axis."…
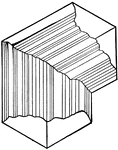
Chalcocite
"Orthorhombic. Usually in small tabular crystals with hexagonal outline. Striated parallel to the brachy-axis.…
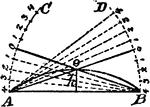
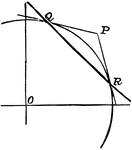
Construction Of A Circle Arc
An illustration showing how to construct a circle arc without recourse to its center, but its chord…
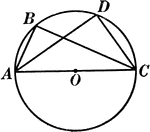
Angles Inscribed in the Same Segment Circle Proof
Illustration of a circle used to prove "All angles inscribed in the same segment are equal."
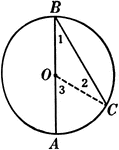
Inscribed Angle in a Circle Proof
Illustration of a circle with an inscribed angle that can be used to prove that "An inscribed angle…
Inscribed Angle in a Circle Proof
Illustration of a circle with an inscribed angle that can be used to prove that "An inscribed angle…
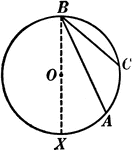
Inscribed Angle in a Circle Proof
Illustration of a circle with an inscribed angle that can be used to prove that "An inscribed angle…
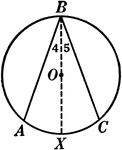
Obtuse Angles Inscribed in Circle Proof
Illustration of a circle used to prove "Any angle inscribed in a segment less than a semicircle is an…
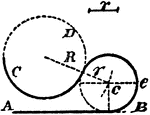
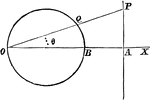
Construction Of A Circle Tangent To A Line And A Circle
An illustration showing how to construct a circle tangent to a given line and given circle. "Add the…
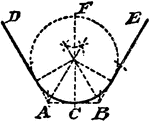
Construction Of A Circle That Tangents 2 Given Lines And Goes Through A Given Point
An illustration showing how to construct a circle that tangents two given lines and goes through a given…
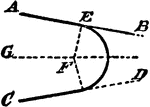
Construction Of A Circle That Tangents 2 Given Lines
An illustration showing how to construct a circle that tangents two given lines inclined to one another…
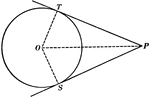
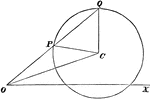
Equal Tangents to Circle Theorem
Illustration used to show that "If two tangents are drawn from any given point to a circle, those tangents…
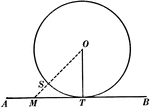
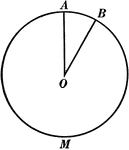
Tangent to Perpendicular Radius Circle Theorem
Illustration used to show that "A tangent to a circle is perpendicular to the radius drawn to the point…

Central Angles and Arcs in a Circle
Illustration of a circle that can be used to show that an "angle at the center of a circle is measured…
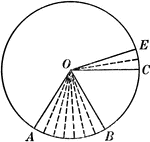
Central Angles and Arcs in a Circle
Illustration of a circle that can be used to show that an "angle at the center of a circle is measured…

Central Angles and Arcs in a Circle
Illustration of a circle that can be used to show that an "angle at the center of a circle is measured…

Chords, Diameters, and Radii of a Circle
Illustration of a circle with diameter AB. Radii are RO, SO, AO, and BO. ED is a chord.
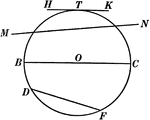
Chords, Secants, Diameters, and Tangents of a Circle
Illustration of a circle with diameter BC, chord DF, secant MN, and tangent HK.
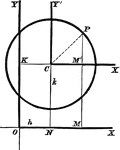
Common Form of Circle
A circle in its common, or central form. This is used to assist students in finding the equation of…
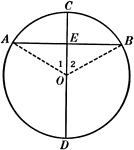
Diameter Perpendicular to a Chord in a Circle
Illustration used to show that "The diameter perpendicular to a chord bisects the chord and also its…
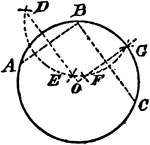
Find The Center Of A Circle Through 3 Points
An illustration showing how to find the center of a circle which will pass through three given points…
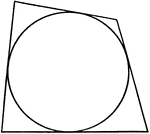
Quadrilateral Circumscribed About a Circle
Illustration of a quadrilateral circumscribed about a circle. This could also be described as a circle…
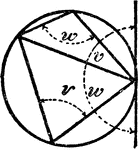
Quadrilateral Inscribed In A Circle
An illustration showing a quadrilateral inscribed in a circle that is tangent to a line.

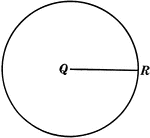
Radius, Diameter, and Chord In A Circle
An illustration showing a circle with radius r, diameter d, and chord c.
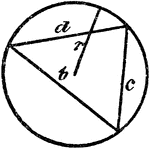
Triangle Inscribed In A Circle
An illustration showing a triangle with sides b, c, and d inscribed in a circle with radius r.
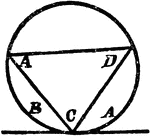
Triangle Inscribed In A Circle
An illustration showing a triangle with angles A, C, and D inscribed in a circle which is tangent to…
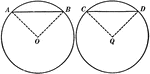
Equal Chords in Equal Circles Theorem
Illustration used to show that "In equal circles, or in the same circle, if two chords are equal, they…
Equal Chords in Equal Circles Theorem
Illustration used to show that "In equal circles, or in the same circle, if two chords are equal, they…

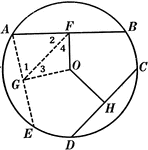
Unequal Chords in Circles Theorem
Illustration used to show that "In equal circles, or in the same circle, if two chords are unequal,…
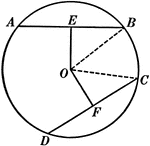
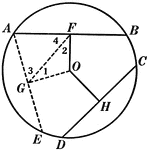
Unequal Chords in Equal Circles Theorem
Illustration used to show that "In equal circles, or in the same circle, if two chords are unequal,…
Unequal Chords in Equal Circles Theorem
Illustration used to show that "In equal circles, or in the same circle, if two chords are unequal,…
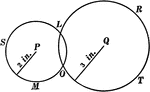
2 Intersecting Circles
Illustration showing a circle with a radius of 2 in. intersecting a circle with a radius of 3 in..
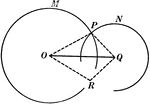
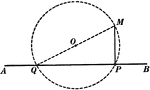
Circumferences of 2 Circles
Illustration used to prove "If two circumferences meet at a point which is not on their line of centers,…

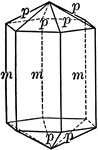
Columbite
"Orthohombic. Habit of crystals is short prismatic; often in square prisms because of prominent development…
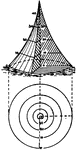
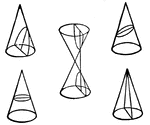
Contours of a concave cone
"The contours of a concave (hollowed out) cone are close together at the center (top), and far apart…
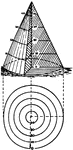
Contours of a cone
The contours of a cone are circles of different sizes, one within another, and the same distance apart,…
Positioning Pen for Constructions
Illustration showing the correct and incorrect position of a right line pen against a T-square, triangle,…

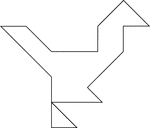
Cormorant
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
Cormorant
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…

Cormorant
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
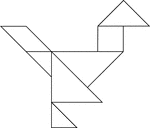
Cormorant
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
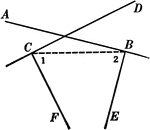
Intersecting Lines Corollary
Illustration used to prove the corollary that "Two lines perpendicular respectively to two intersecting…
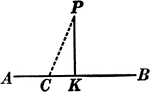
Perpendicular to Line Corollary
Illustration used to prove the corollary that "From a point outside a line there exists only one perpendicular…
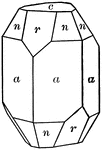
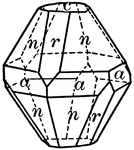
Corundum
"Hexagonal-rhombohedral. Crystals usually prismatic in habit or tapering hexagonal pyramids." —…
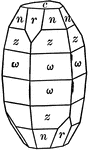
Corundum
"Hexagonal-rhombohedral. Crystals usually prismatic in habit or tapering hexagonal pyramids." —…