Clipart tagged: ‘pulmonary’
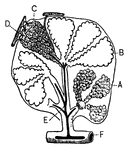
Capillaries of the Air Sac
"Diagram showing the capillary network of the air sacs and origin of the pulmonary veins.. A,…

Muscular fibers of the auricle
L.A., left auricle; R.A., right auricle; A, opening of the inferior vena…
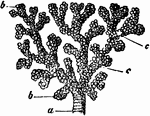
A Bronchial Tube
A small bronchial tube. Labels: a, dividing into its terminal branches, c; these have pouched or sacculated…

Diagram of the circulation of the blood
"R.A., right auricle; L.A., left auricle; R.V., right ventricle; L.V.,…

Gills (Branchial Arch of Perch)
This illustration shows the gills (breathing apparatus) of a perch, as well as the specific veins and…

Gills (Crayfish)
This illustration shows the thorax of a crayfish with a portion of the carapace removed to show the…

Heart and Lungs
1, The trachea or windpipe; 2 and 3, right and left common carotid arteries; 4 and 5, right and left…
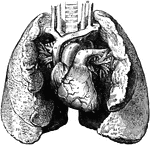
Heart and Lungs
The heart and lungs. 1, right ventricle; 3, right auricle (atrium); 6, 7, pulmonary artery; 9, aorta;…
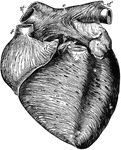
Anterior View of the Heart
Anterior view of the heart, dissected, after long boiling to show the superficial muscular fibers. The…
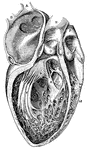
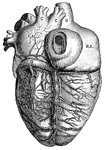
Cavities of the heart
"A, B, right pulmonary veins, S, openings of the left pulmonary veins; E, D, C,…
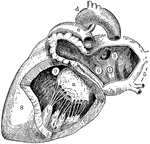
Left Side of Heart
Left side of heart. Labels: 1, cavity of left auricle (atrium); 3, opening of right pulmonary veins;…
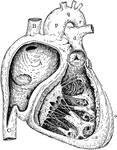
Right Side of Heart
Right side of heart. Labels: A, cavity of right ventricle; B, superior vena cava; C, inferior vena cava;…
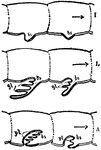
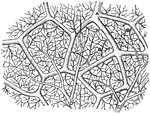
Lamellae
"Diagram to show the way in which an outgrowing gill-process bearing blood-holding lamellae, may give…
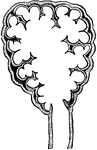
Pulmonary lobule
"Section of a pulmonary lobule, showing its division into pulmonary vesicles." — Tracy, 1888
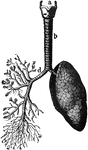
Lungs and Air Passages
The lungs and air passages seen from the front. On the left of the figure the pulmonary tissue has been…

The Lungs and Air Passages
The lungs and air passages seen from the front. On the left of the figure the pulmonary tissue has been…
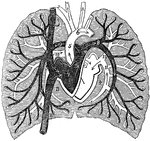
A Diagram of Pulmonary Circulation
A diagram of pulmonary circulation. Labels: 1, Descending vena cava. 2, Ascending cava vein. 3, Chamber…
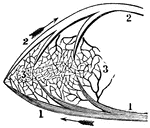
A Portion of the Pulmonic Circulation
A portion of the pulmonic circulation. 1, A branch of the artery that carries the impure blood to the…
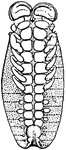
Scorpio Embryo
"Embryo of scorpion, ventral view showing somites and appendages. sgc, Frontal groove. sa, Rudiment…
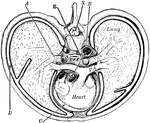
Thorax
"Cross-section of thorax. A, bronchus, entering the lung; B, the aorta cut at its origin and again at…
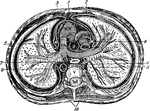
Transverse Section of the Thorax
Transverse section of the thorax. Labels: 1, anterior mediastinum; 2, internal mammary vessels; 3, triangularis…