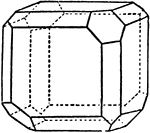
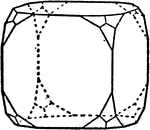
Cube trunctuated by octahedron
"When a corner or an edge of one form is replaced by a face of another form, the first is said to be…
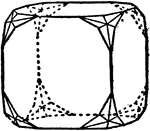
Octahedron trunctuated by cube
"When a corner or an edge of one form is replaced by a face of another form, the first is said to be…
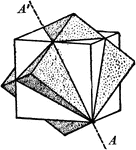
Twinned cubes
"A penetration twin, since the two individuals interpenetrate each other." — Ford, 1912
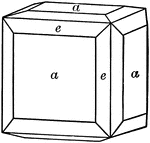
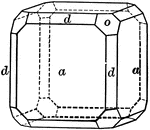
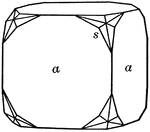
Cube and tetrahexahedron
"A cube with its edges beveled by the faces of a tetrahexahedron." — Ford, 1912
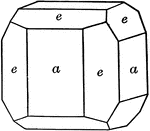
Cube and pyritohedron
"A combination of cube and pyritohedron, in which it will be noted that the faces of the pyritohedron…
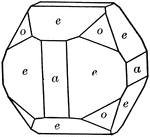
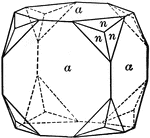
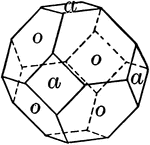
Pyritohedron, cube, and octahedron
"A cube trunctuated with pyritohedron and octahedron." — Ford, 1912

Cube and tetrahedron
"A combination of cube and tetrahedron. It will be noted that the tetrahedron faces truncate the alternate…
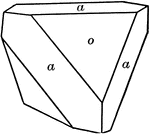
Tetrahedron and cube
"A combination of cube and tetrahedron. It will be noted that the tetrahedron faces truncate the alternate…
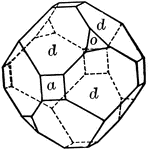
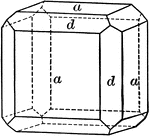
Cube, dodecahedron and tetrahedron
"A combination of cube, dodecahedron, and tetrahedron." — Ford, 1912
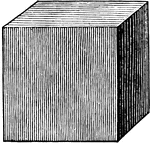
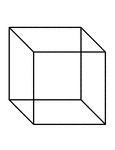
Cube
A regular body with six square faces; a rectangular parallelopiped, having all its edges equal.
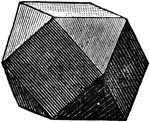
Cuboctahedron
A solid with fourteen faces formed by cutting off the corners of a cube parallel to the coxial octahedron…

Cube
"Science has succeeded in classifying the thousands of known crystals in six systems, to each of which…

Transit Instrument
"One of the most important of astronomical instruments, consists of a telescope fixed to a horizontal…

Primitive Crystal
"In this the four lateral planes are rectangular and equal; they may be either oblong or square; in…
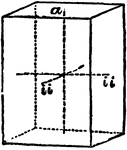
Primitive Crystal
"If the base is a square and the prism stands erect—that is, if its sides or lateral planes, as…
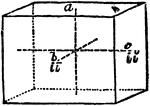
Primitive Crystal
"When the base is a rectangle instead of a square, the form is a right rectangular prism." —The…
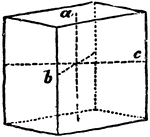
Primitive Crystal
"When the base is a rhombus, and the prism stands erect, the form is a right rhombic prism." —The…
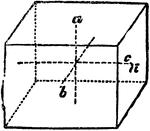
Primitive Crystal
"When the base is a rhomboid, and the prism stands erect, it is only the opposite laeral faces that…

Angular Perspective
This object is a cube, having therefore all its faces of equal dimensions; and as both sides recede,…
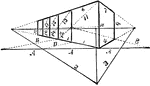
Angular Perspective
This cube has four additional cubes of equal dimensions. This is effected by first drawing the cube…
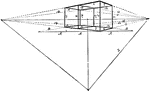
Angular Perspective
This figure differs from the others because they are solid cubes. Further, the geometrical scale is…

Nasik Cube
Squares that have many more summations than just rows, columns, and diagonals. Frost extended this idea…
Shear
"Shear is a particular form of strain produced by causing plane layers of a material to slide parallel…
Cube in Combination with Octahedron
Represents the combination of an octrahedron and a cube, with the cube faces predominate.
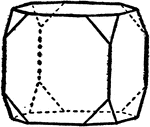
Cubo-octahedron
Represents the combination of a cube and an octahedron, with both faces being equal.
Octahedron in Combination with Cube
Represents the combination of an octahedron and a cube, with the octahedron predominate.
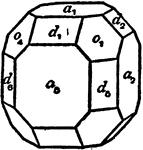
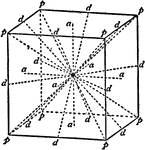
Clinographic Drawing of a Cubic Crystal
"A drawing of a crystal showing a combination of the cube, octahedron and rhombic dodecahedron is shown,…
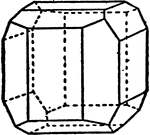
Combination of Pentagonal Dodecahedron and Cube
Represents a combination of a pentagonal dodecahedron and cube, and are common in pyrites.
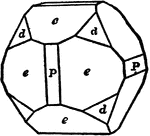
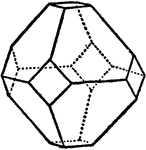
Combination of Pentagonal Dodecahedron, Cube and Octahedron
Represents the combination of pentagonal dodecahedron, cube, and octahedron.
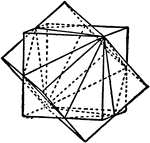
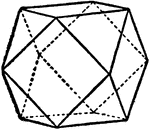
Interpenetrating Twinned Cubes
"Here one cube may be brought into the position of the other by a rotation of 180 degrees about a traid…

Archimedies Principle
"It is evident that, when a solid is immersed in a fluid, it will displace exactly its own volume of…

Cube
"A cube is a prism whose faces are ends are squares. All the faces of a cube are equal." —Hallock…