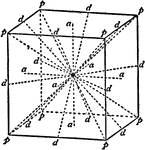
Symmetry axis
"A crystal has a center of symmetry if an imaginary line is passed from some point on its surface through…
Symmetry center
"A crystal has a center of symmetry if an imaginary line is passed from some point on its surface through…
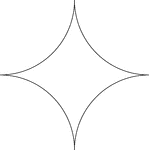
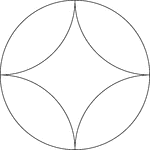
Reflected Arcs Of A Circle
A design created by dividing a circle into 4 equal arcs and reflecting each arc toward the center of…
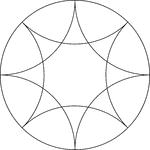
Reflected Arcs Of 2 Circles In A Circle
A design created by dividing a circle into 4 equal arcs and creating a reflection of each arc toward…
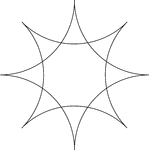
Reflected Arcs Of 2 Circles
A design created by dividing a circle into 4 equal arcs and reflecting each arc toward the center of…
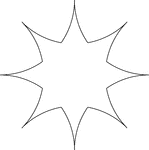
Reflected Arcs Of 2 Circles
A design created by dividing a circle into 4 equal arcs and reflecting each arc toward the center of…

Reflected Arcs Of 4 Circles In A Circle
A design created by dividing a circle into 4 equal arcs and creating a reflection of each arc toward…
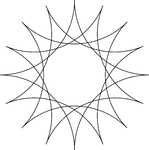
Reflected Arcs Of 4 Circles In A Circle
A design created by dividing a circle into 4 equal arcs and creating a reflection of each arc toward…

Reflected Arcs Of 8 Circles In A Circle
A design created by dividing a circle into 4 equal arcs and creating a reflection of each arc toward…

Reflected Arcs Of 8 Circles
A design created by dividing a circle into 4 equal arcs and creating a reflection of each arc toward…
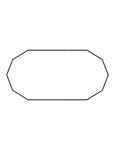
Irregular Convex Decagon
Illustration of an irregular convex decagon. This polygon has some symmetry.
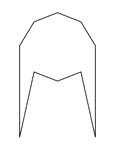
Irregular Convex Decagon
Illustration of an irregular convex decagon. This polygon has some symmetry.
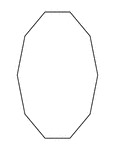
Irregular Convex Decagon
Illustration of an irregular convex decagon. This polygon has some symmetry.
Irregular Convex Decagon
Illustration of an irregular convex decagon. This polygon has some symmetry.
Irregular Convex Decagon
Illustration of an irregular convex decagon. This polygon has some symmetry.

Concave Equilateral Dodecagon
A 6-point star made from a non-regular concave dodecagon in which all sides are equal in length. There…
Irregular Convex Dodecagon
Illustration of an irregular convex dodecagon. This polygon has some symmetry.
Irregular Convex Dodecagon
Illustration of an irregular convex dodecagon. This polygon has some symmetry.
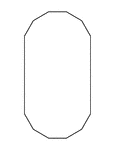
Irregular Convex Dodecagon
Illustration of an irregular convex dodecagon. This polygon has some symmetry.
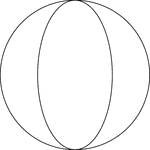
Ellipse Inscribed In A Circle
Illustration of an ellipse, whose major axis is vertical, inscribed in a circle whose diameter is equal…
16 Rotated Concentric Ellipses
Illustration of 16 concentric congruent ellipses that are rotated about the center at equal intervals…
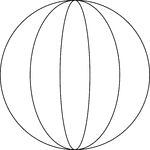
2 Ellipses Inscribed In A Circle
Illustration of 2 concentric ellipses, whose major axes are vertical, inscribed in a circle whose diameter…

2 Rotated Concentric Ellipses
Illustration of 2 concentric congruent ellipses that are rotated about the center at 90°. The ellipses…
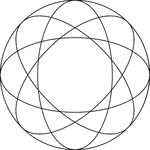
4 Rotated Concentric Ellipses
Illustration of 4 concentric congruent ellipses that are rotated about the center at equal intervals…
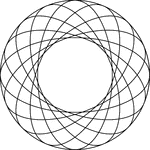
8 Rotated Concentric Ellipses
Illustration of 8 concentric congruent ellipses that are rotated about the center at equal intervals…
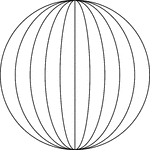
Ellipses Inscribed In A Circle
Illustration of concentric ellipses, whose major axes are vertical, inscribed in a circle whose diameter…
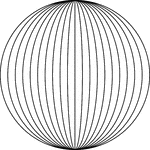
Ellipses Inscribed In A Circle
Illustration of concentric ellipses, whose major axes are vertical, inscribed in a circle whose diameter…
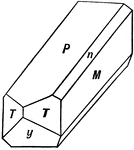
Elongation in the Direction of the Clinodiagonal Axis
In cases where the basal pinacoid is fixed by some physical property like cleavage, the elongation is…
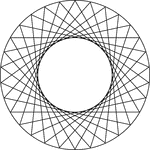
10 Congruent Rotated Equilateral Triangles
Illustration of 10 congruent equilateral triangles that have the same center. Each triangle has been…
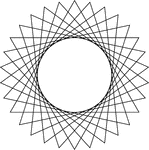
10 Congruent Rotated Equilateral Triangles
Illustration of 10 congruent equilateral triangles that have the same center. Each triangle has been…
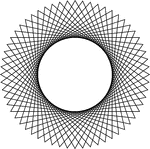
20 Congruent Rotated Equilateral Triangles
Illustration of 20 congruent equilateral triangles that have the same center. Each triangle has been…

5 Congruent Rotated Equilateral Triangles
Illustration of 5 congruent equilateral triangles that have the same center. Each triangle has been…
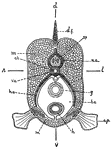
Fish
This is a diagram of the cross section of a fish, showing the bilateral symmetry of the parts: dv, dorsoventral…
Irregular Convex Heptagon
Illustration of an irregular convex heptagon. This polygon has some symmetry.
Irregular Convex Heptagon
Illustration of an irregular convex heptagon. This polygon has some symmetry.
Irregular Convex Heptagon
Illustration of an irregular convex heptagon. This polygon has some symmetry.

Irregular Convex Heptagon
Illustration of an irregular convex heptagon. This polygon has some symmetry.
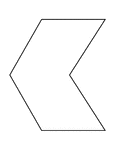
Irregular Concave Hexagon
Illustration of an irregular hexagon. This is also an example of a concave polygon with symmetry.
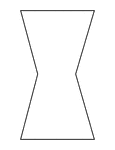
Irregular Concave Hexagon
Illustration of an irregular hexagon. This is also an example of a concave polygon with symmetry.
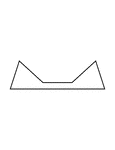
Irregular Concave Hexagon
Illustration of an irregular hexagon. This is also an example of a concave polygon with symmetry.
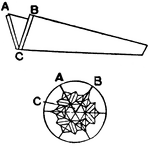
Mirrors in a Kaleidoscope
This illustration shows the arrangement of mirrors in a kaleidoscope (AC and BC), and the patterns formed.
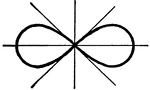
Lemniscate
A Lemniscate is, in general, a curve generated by a point moving so that the product of its distances…
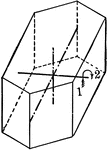
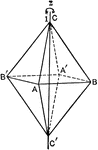
Symmetry of monoclinic system
"The symmetry of the Monoclinic System is as follows: The crystallographic axis b is an axis of binary…
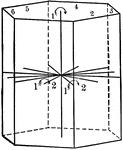
Symmetry of normal class
"The symmetry of the Normal Class of the Hexagonal System is as follows: The vertical crystallographic…
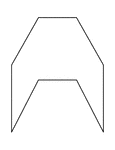
Irregular Concave Octagon
Illustration of an irregular concave octagon. This polygon has some symmetry.
Irregular Concave Octagon
Illustration of an irregular concave octagon. This polygon has some symmetry.

Irregular Concave Octagon
Illustration of an irregular concave octagon. This polygon has some symmetry.
Irregular Convex Octagon
Illustration of an irregular convex octagon. This polygon has some symmetry.
Irregular Convex Octagon
Illustration of an irregular convex octagon. This polygon has some symmetry.
Irregular Convex Octagon
Illustration of an irregular convex octagon. This polygon has some symmetry.
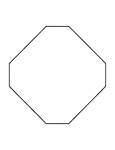
Irregular Convex Octagon
Illustration of an irregular convex octagon. This polygon has some symmetry.
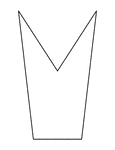
Irregular Concave Pentagon
Illustration of an irregular pentagon. This is also an example of a concave polygon with symmetry.

Irregular Convex Pentagon
Illustration of an irregular pentagon. This is also an example of a convex polygon with symmetry.
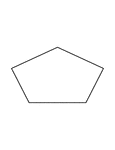
Irregular Convex Pentagon
Illustration of an irregular pentagon. This is also an example of a convex polygon with symmetry.
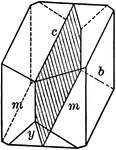
Symmetry plane
"A crystal has a center of symmetry if an imaginary line is passed from some point on its surface through…
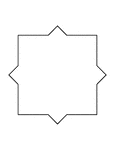
Irregular Convex Polygon
Illustration of an irregular convex polygon with 16 sides that has symmetry. It could be used to show…
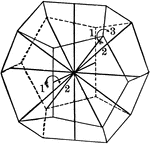
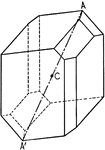
Symmetry of pyritohedral class
"The symmetry of the Pyritohedral class is as follows: The three crystal axes of binary symmetry; the…