Clipart tagged: ‘tetrahedron’
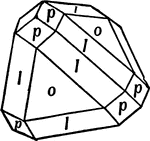
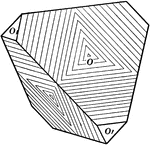
Beveled Tetrahedron
This form shows a tetrahedron (o) with its edges beveled by the trigonal tristetrahedron (l), and its…
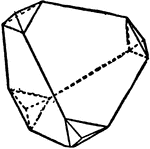
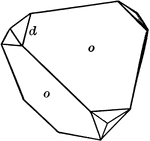
Combination of Tetrahedron and Rhombic Dodecahedron
A combination of a tetrahedron and a rhombic dodecahedron.
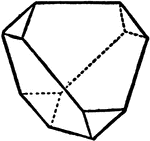
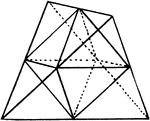
Combination of two Tetrahedra
"...a combination of these two tetrahedra, and represents a crystal of blende, in which the four larger…

Cube and tetrahedron
"A combination of cube and tetrahedron. It will be noted that the tetrahedron faces truncate the alternate…
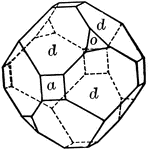
Cube, dodecahedron and tetrahedron
"A combination of cube, dodecahedron, and tetrahedron." — Ford, 1912

Regular Polyhedrons
Illustration of regular polyhedrons: tetrahedron, hexahedron, octahedron, dodecahedron, icosahedron.
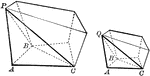
Two Similar Polyhedrons
Diagram used to prove the theorem: "Two similar polyhedrons may be decomposed into the same number of…
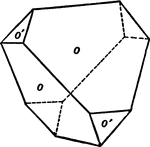
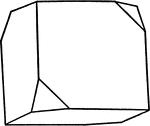
Positive and Negative Tetrahedron in Combination
This form shows a positive and negative tetrahedron in combination.
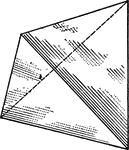
Regular Tetrahedron
"Science has succeeded in classifying the thousands of known crystals in six systems, to each of which…
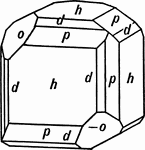
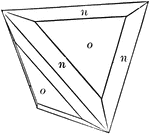
Sodium Chlorate
This is a crystal of Sodium Chlorate, exhibiting the tetrahedron (-o) and the pentagonal dodecahedron…

Various Solid Forms
Illustration containing a tetrahedron, hexahedron, octahedron, dodecahedron, and icosahedron, placed…
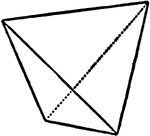
Tetrahedron
"This is bounded by four equilateral triangles and is identical with the regular tetrahedron of geometry."…
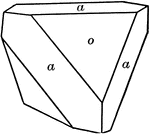
Tetrahedron and cube
"A combination of cube and tetrahedron. It will be noted that the tetrahedron faces truncate the alternate…
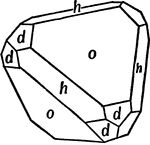
Tetrahedron, Cube, and Dodecahedron in Combination
This form shows a tetrahedron (o), cube (h), and dodecahedron (d) in combination.

Negative tetrahedron
"The tetrahedron is a form composed of four equilateral triangular faces, each of which intersects all…
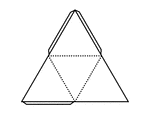
Pattern for Tetrahedron
Pattern that can be cut out and folded to construct a regular tetrahedron. Fold on the dotted lines,…

Positive tetrahedron
"The tetrahedron is a form composed of four equilateral triangular faces, each of which intersects all…
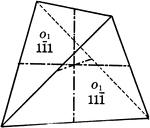
Positive and negative tetrahedrons
"If a positive and negative tetrahedron occured together with equal development, the resulting crystal…
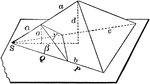
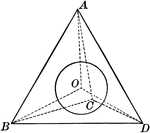
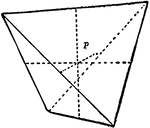
Two Proportional Tetrahedrons
Diagram used to prove the theorem: "Two tetrahedrons having a trihedral angle in each equal, are to…