This mathematics ClipArt gallery offers 87 illustrations of analytical geometry, which is also called coordinate geometry, Cartesian geometry, algebraic geometry, or simply analytic geometry. It is the study of geometry using principles of algebra.
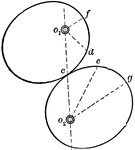
Rolling of Non-cylindrical Surfaces
Illustration showing that the rolling of non-cylindrical surfaces. "If the angular velocity ratio of…
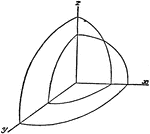
Octant of Wave Surface
the octant of the wave surface cuts each coordinate plane in a circle and an ellipse.
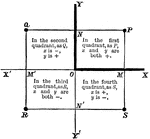
Coordinate Plane
A coordinate planes with the quadrants labeled showing which value (x or y) is positive or negative.
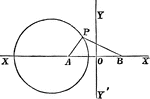
Coordinate Plane
A circle with part of a triangle inscribed in it. They are lying on a coordinate plane.
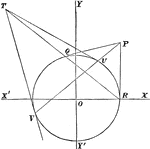
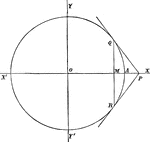
Polar Property
If the chords of a circle are drawn through a fixed point, then the points of intersection of the pairs…
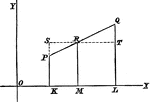
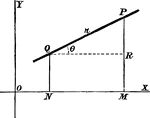
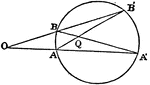
Point Ratio
Showing how to find points on a coordinate plane. Also, shows an example of the midpoint formula.

Vector Addition Given Resultant
Illustration "where ad is the given resultant, if the two components have the magnitudes represented…
Vector Motion Into Two Components - Resultant
Illustration used to resolve a motion into two components, one of which is perpendicular, and the other…

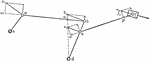
Velocities Of Rigidly-connected Points
Illustration for rigidly-connected points. "If two points are so connected that their distance apart…
Velocities Of Rigidly-connected Points
Illustration for rigidly-connected points. In the series of links shown, c and d are fixed axes and…
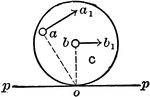
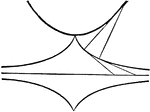
Section of Rolling Surfaces
Illustration showing a section of the rolling surfaces by a plane perpendicular to their straight line…

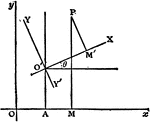
Construction Of Shield's Anti-friction Curve
An illustration showing how to construct Shield's anti-friction curve. "R represents the radius of the…
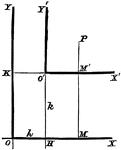
Axes Shift
Any system of coordinate axes to another set which is parallel to the former, but with different origins.
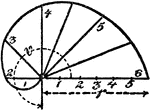
Construction Of An Arithmetic Spiral
An illustration showing how to construct an arithmetic spiral. "Given the pitch p and angle v, divide…
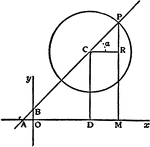
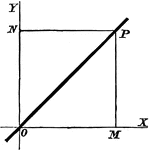
Straight Line
The straight line is the simplest type of locus and the simplest first degree equation.
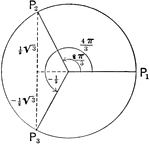
Cubed Roots of Unity
Illustration showing how to find the cubed roots of unity by applying DeMoivre's Theorem.

Fifth Roots of Unity
Illustration showing how to find the fifth roots of unity by applying DeMoivre's Theorem.

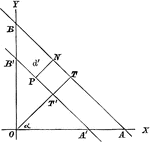
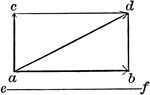
Vector Addition
Illustration showing two component forces ab and ac acting upon point a. The result is the vector ad…