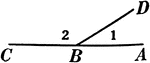
Open Stepladder
Illustration of a stepladder that is opened to form an isosceles triangle with the ground.
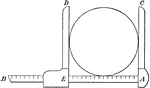
Skyscraper Giant Stepladder
Illustration of a giant stepladder, sometimes called a skyscraper stepladder, that is opened next to…

Open Stepladder
Illustration of a stepladder that is opened to form an isosceles triangle with the ground.

Unit Circle
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane. The…
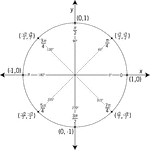
Unit Circle Labeled In 45 ° Increments
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
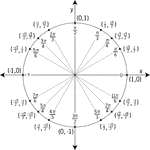
Unit Circle Labeled With Special Angles And Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
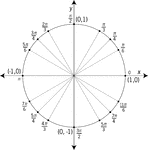
Unit Circle Labeled At Special Angles
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…

Unit Circle Labeled At Special Angles
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
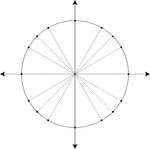
Unit Circle Marked At Special Angles
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane. All…
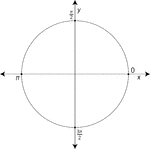
Unit Circle Labeled At Quadrantal Angles
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
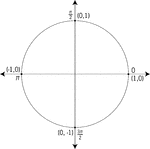
Unit Circle Labeled With Quadrantal Angles And Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane. All…
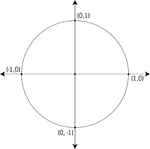
Unit Circle Labeled With Quadrantal Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane. At each…
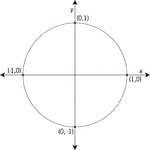
Unit Circle Labeled With Quadrantal Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
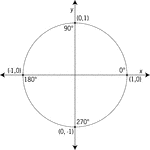
Unit Circle Labeled With Quadrantal Angles And Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
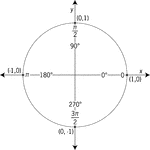
Unit Circle Labeled With Quadrantal Angles And Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
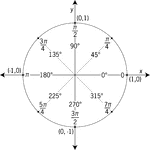
Unit Circle Labeled In 45° Increments With Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
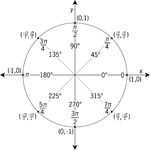
Unit Circle Labeled In 45° Increments With Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
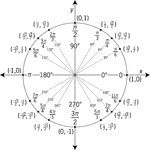
Unit Circle Labeled With Special Angles And Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
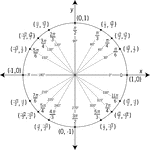
Unit Circle Labeled With Special Angles And Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
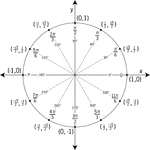
Unit Circle Labeled In 30° Increments With Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
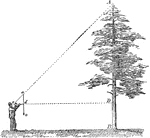
Measuring Tree Height
A man measuring the height of a tree by determining the angle and how far away he is standing.
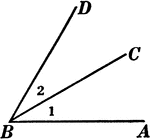
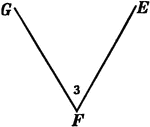
Adjacent Angles
Angles 1 and 2 are adjacent angles. Two angles with a common vertex and a common side between them are…
Difference of Angles
Illustration showing that the difference between angle 1 and angle 2 is angle ABC.
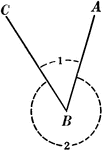
Acute and Reflex Angles
Illustration showing two positive angles; angle 1 being the acute angle and angle 2 being the reflex…
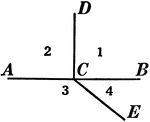
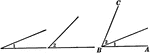
Relationships Between 4 Angles
Illustration showing four angles that can be used to define different relationships, such as adjacent,…
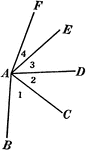
Relationships Between 4 Angles
Illustration showing four angles that can be used to define different relationships, such as adjacent,…

Supplementary and Right Angles
Illustration showing angles 1 and 2 are supplementary and angles ACD and DCB are supplementary. Also,…

Vertical Angles
Illustration showing that angles 1 and 2 are vertical and angles 3 and 4 are vertical.
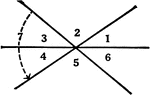
Relationships Between 6 Angles
Illustration showing six angles that can be used to define different relationships, such as adjacent,…

Optical Illusions
Illustration showing optical illusions. It is not always possible to trust the eye to be sure if the…

Optical Illusions
Illustration showing optical illusions. It is not always possible to trust the eye to be sure if the…
Optical Illusions
Illustration showing optical illusions. It is not always possible to trust the eye to be sure if the…

Optical Illusions
Illustration showing optical illusions. It is not always possible to trust the eye to be sure if the…
Optical Illusions
Illustration showing optical illusions. It is not always possible to trust the eye to be sure if the…
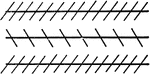
Optical Illusions
Illustration showing optical illusions. It is not always possible to trust the eye to be sure if the…
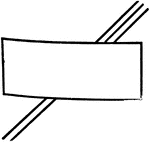
Optical Illusions
Illustration showing optical illusions. It is not always possible to trust the eye to be sure if the…
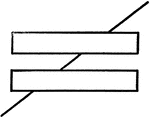
Optical Illusions
Illustration showing optical illusions. It is not always possible to trust the eye to be sure if the…
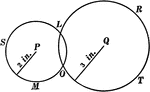
2 Intersecting Circles
Illustration showing a circle with a radius of 2 in. intersecting a circle with a radius of 3 in..
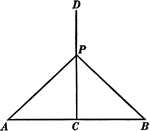
Triangle With Perpendicular Bisector
Illustration showing a perpendicular bisector of a triangle extended outside of the triangle.

Construction Of A Perpendicular Bisector Of A Straight Line
Illustration of the construction used to make a perpendicular bisector of a straight line.
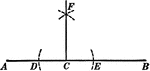
Construction Of A Perpendicular To A Straight Line
Illustration of the construction used to create a perpendicular to a straight line at a given point.
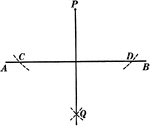
Construction Of A Perpendicular To A Straight Line
Illustration of the construction used to create a perpendicular to a straight line from a given point…
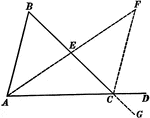
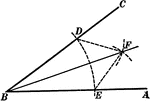
Exterior Angle of Triangle Theorem
Illustration used to prove that "If one side of a triangle is prolonged, the exterior angle formed is…