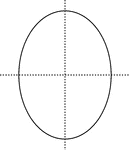
Lines of Symmetry, Oval With
Oval with dotted vertical and horizontal lines that are lines of symmetry.
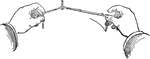
Drop Pen
Drop pen, or rivet pen, can make small circles faster than the bow pen. The pen is useful in bridge…

Drawing a Circle Using Compass
When drawing the circle, the compass is turned by the handle with the thumb and forefinger in a clockwise…
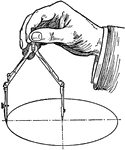
Drawing Large Circles with Compass
"Circles up to perhaps three inches in diameter may be drawn with the legs straight but for larger sizes…

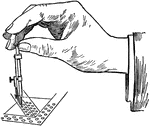
Drawing Small Circles with Bow Instrument
Bow instruments can be used for drawing small circles. Hold the the left hand and spin the nut in or…
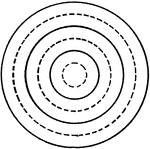
Drawing Concentric Circles with Compass
"Draw Horizontal line throuch center of space. On it mark off radii for six concentric circles 1/4"…
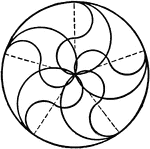
Drawing Tangent Arcs with Compass and Dividers
"Draw a circle three inches in diameter. Divide the circumference into five equal parts by trial with…
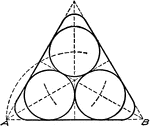
Drawing Tangent Circles and Lines with Compass and Triangles
"On base AB, 3 1/2" long construct an equilateral triangle, using the 60-degree triangle. Bisect the…
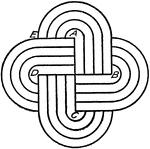
Drawing Tangent to Circle Arcs with Bow Compass
"Draw one and one-half inch square about center of space. Divide AE into four 3/16" spaces, with scale.…
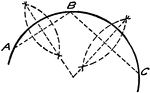
Draw Circular Arc Through Three Given Points
"Join AB and BC, bisect AB and BC by perpendiculars. Their intersection will be the center of the required…
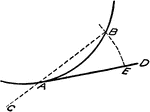
Approximating Length of Circle Arc using Straight Line
"At A draw the tangent AD and Chord AB produced. Lay off AC equal to half the chord AB. With center…
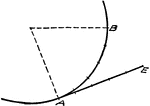
Rectifying Arc Using Dividers
"In ordinary work the usual way of rectifying an arc is to step around it with the dividers, in spaces…

Conic Section Using Circle
The cone is sliced by a circle in a plane perpendicular to the axis. This can be drawn without knowledge…

Conic Section Using Ellipse
The cone is sliced by a ellipse by making an angle within the plane. This can be drawn with knowing…
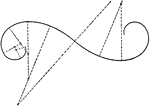
Curve Inked with Circle Arcs
"Any noncircular curve may be approximated by tangent circle arcs, selecting a center by trial, drawing…
Cycloid
"A cycloid is the curve generated by the motion of a point on the circumference of a circle rolled along…

Epicycloid and Hypocycloid
Epicycloid is generated by a circle rolled outside of another circle, whereas a hypocycloid is circle…
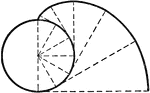
Involute of Circle
"A circle may be conceived as a polygon of an infinite number of sides. Thus to draw the involute of…
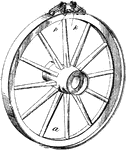
Adjustable Tire
A tire is ring shaped, the earliest tires were bands of iron placed on wooden wheels which were used…

Shading a Circle Using Compass
"A circle may be shaded by shifting the center on a 45-degree line toward the lower right hand corner...…
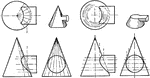
Development of Cone
A rolled out image of a cone by dividing the base in equal parts and arcs to measure the true lengths.
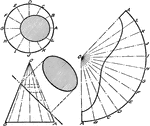
Development of Sphere Gore Method
An illustration in flattening the sphere using Gore method by creating cylinder sections with equal…
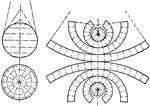
Development of Sphere Zone Method
An illustration of a development of sphere using Zone method by creating sections of rolled out cones.
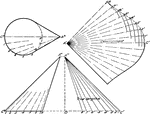
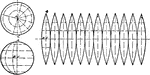
Development of Oblique Cone by Triangulation
A development or rolled out oblique cone using triangulation. The method of triangulation is done by…
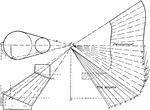
Oblique Cone by Triangulation Connecting to Two Parallel Pipes of Different Diameters
"An oblique cone connecting two parallel pipes of different diameters... the true size of the base is…
Intersection of Cylinder and Cone
An illustration of finding an intersection of a cone and cylinder by either cutting the vertex of the…
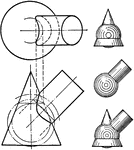
Intersection of Cylinder and Cone
An illustration of finding an intersection of a cone and cylinder by either cutting the vertex of the…
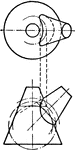
Intersection of Two Cones
"The cone B would be developed by cutting a right section as S—S whose stretchout will be a circle…
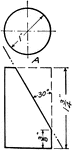
Development Exercise of Cylinder
An exercise problem in creating a development or rolled out surface of a cylinder in a 4" by 5" drawing…
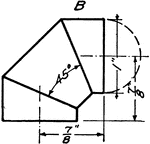
Development Exercise of Cylinder using Three Piece Elbow
The exercise problem of creating a three piece elbow development or rolled out image of the cylinder…
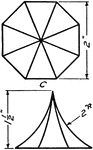
Development Exercise of Octagonal Roof and True Shape of Rafter
Problem exercise in drawing a development or a stretchout image of the octagonal roof and finding the…
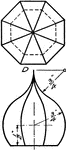
Development Exercise of Dome and True Shape of Hip
A development or rolled out image exercise problem of the dome and finding the true shape of the hip,…
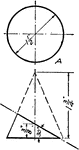
Development Exercise of Cone
Development and top completion exercise problem of the cone by dividing the base into equal parts and…
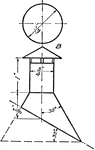
Development Exercise of Flange and Hood Cones
An exercise problem to complete the top and develop, stretched out, image of the flange and hood cones…