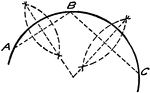
Draw Circular Arc Through Three Given Points
"Join AB and BC, bisect AB and BC by perpendiculars. Their intersection will be the center of the required…
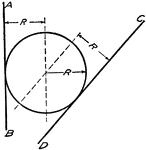
Draw Arc of Given radius R Tangent to Two Given Lines
"Draw lines parallel to AB and CD at distant R from them. The intersection of these lines will be center…
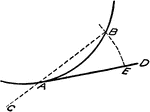
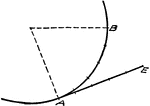
Approximating Length of Circle Arc using Straight Line
"At A draw the tangent AD and Chord AB produced. Lay off AC equal to half the chord AB. With center…
Rectifying Arc Using Dividers
"In ordinary work the usual way of rectifying an arc is to step around it with the dividers, in spaces…

Conic Section Using Circle
The cone is sliced by a circle in a plane perpendicular to the axis. This can be drawn without knowledge…

Conic Section Using Ellipse
The cone is sliced by a ellipse by making an angle within the plane. This can be drawn with knowing…
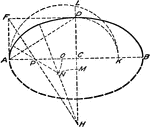
Approximate Ellipse with Five Centered Arc
"This (five centered arc) method is based on the principle that the radius of curvature at the end of…
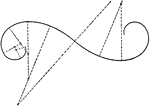
Curve Inked with Circle Arcs
"Any noncircular curve may be approximated by tangent circle arcs, selecting a center by trial, drawing…
Cycloid
"A cycloid is the curve generated by the motion of a point on the circumference of a circle rolled along…

Epicycloid and Hypocycloid
Epicycloid is generated by a circle rolled outside of another circle, whereas a hypocycloid is circle…
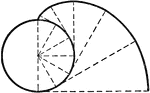
Involute of Circle
"A circle may be conceived as a polygon of an infinite number of sides. Thus to draw the involute of…
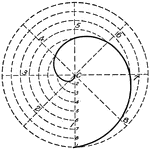
Draw Spiral of Archimedes
"Divide the circumference into a number of equal parts, drawing the radii and numbering the points.…
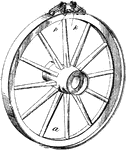
Adjustable Tire
A tire is ring shaped, the earliest tires were bands of iron placed on wooden wheels which were used…
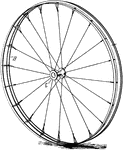
Side View of a Vehicle Wheel
A wheel is a circular device that is capable of rotating on its axis, facilitating movement and transportation.

Shading a Circle Using Compass
"A circle may be shaded by shifting the center on a 45-degree line toward the lower right hand corner...…
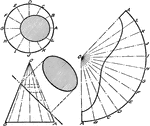
Development of Cone
A rolled out image of a cone by dividing the base in equal parts and arcs to measure the true lengths.
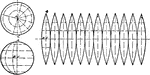
Development of Sphere Gore Method
An illustration in flattening the sphere using Gore method by creating cylinder sections with equal…
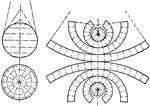
Development of Sphere Zone Method
An illustration of a development of sphere using Zone method by creating sections of rolled out cones.
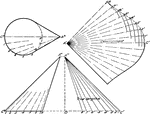
Development of Oblique Cone by Triangulation
A development or rolled out oblique cone using triangulation. The method of triangulation is done by…
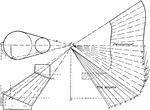
Oblique Cone by Triangulation Connecting to Two Parallel Pipes of Different Diameters
"An oblique cone connecting two parallel pipes of different diameters... the true size of the base is…
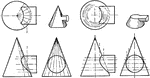
Intersection of Cylinder and Cone
An illustration of finding an intersection of a cone and cylinder by either cutting the vertex of the…
Intersection of Cylinder and Cone
An illustration of finding an intersection of a cone and cylinder by either cutting the vertex of the…
Intersection of Two Cones
"The cone B would be developed by cutting a right section as S—S whose stretchout will be a circle…
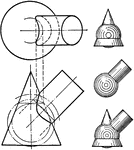
Development Exercise of Cylinder
An exercise problem in creating a development or rolled out surface of a cylinder in a 4" by 5" drawing…
Development Exercise of Cylinder using Three Piece Elbow
The exercise problem of creating a three piece elbow development or rolled out image of the cylinder…
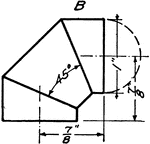
Development Exercise of Octagonal Roof and True Shape of Rafter
Problem exercise in drawing a development or a stretchout image of the octagonal roof and finding the…
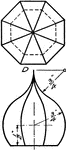
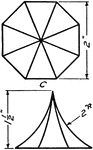
Development Exercise of Dome and True Shape of Hip
A development or rolled out image exercise problem of the dome and finding the true shape of the hip,…
Development Exercise of Cone
Development and top completion exercise problem of the cone by dividing the base into equal parts and…
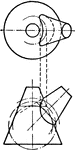
Development Exercise of Flange and Hood Cones
An exercise problem to complete the top and develop, stretched out, image of the flange and hood cones…
Cookie Mold Cutter
Many decorating techniques used today do not require elaborate cookie cutters. The simplest of shapes…
Star Shaped Cookie Cutter
Many decorating techniques used today do not require elaborate cookie cutters. The simplest of shapes…
Circle Aerodynamic
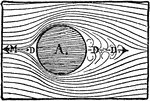
A circle in a aerodynamic chamber where the airflow hitting the object. The area at point DD is large…
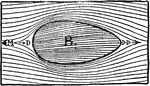
Ellipse Aerodynamic
Aerodynamic of the ellipse where the area at point DD is small. The small area creates less resistance…

Aeroplane Nose Spin Dive Flying
The illustration of the plane descending while spiraling down. The radius of the spiral spin is getting…
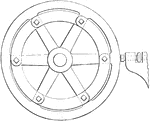
Turning Hand Wheels
An illustration of creating a hand wheel by spinning while moving threaded tool to the desired radius.
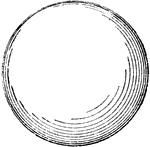
Wooden Sphere
A wooden hollow sphere created by using a lathe and wooden templet at a desired diameter.
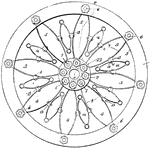
Eight Spoke Wheel
A wheel is a circular device that is capable of rotating on its axis, facilitating movement or transportation…

Isometric Drawing of Circle using Square
The illustration of constructing a circle or ellipse using isometric drawing. The inscribed circle is…
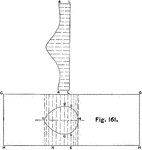
Development of Two Intersecting Cylinder
A development, or rolled out image, of two cylinders intersecting each other. The large rectangular…
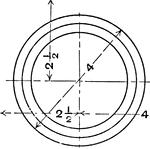
Drawing Exercise Eight Concentric Circles using Ink
A drawing exercise for drawing eight concentric circles by dividing the paper in quarters as shown.…

Dotted Lined Eight Concentric Circles using Ink and Pencil Drawing Exercise
Mechanical drawing exercise of drawing dotted lined concentric circles. The circles are first drawn…
Drawing Exercise of Inscribed Circle Pattern Tangent to Left Side
An inscribed circle pattern exercise for mechanical drawing. The pattern is drawn by dividing the horizontal…
Mechanical Drawing Exercise Circle with Wavy Curved Lines Inside
A mechanical drawing exercise of a circle with curved wavy lines. The image is drawn by dividing horizontal…
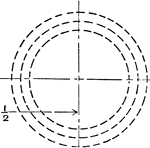
Inscribed Circle with Smaller Circles at Tangent Points Both Sides of the Large Circle Mechanical Drawing Exercise
Mechanical drawing exercise for circle with two tangent points on both sides of the circle. The paper…
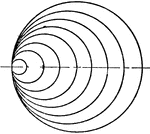
Curved Line with Circle Mechanical Drawing Exercise
A mechanical drawing exercise of drawing a curved line with circle in the middle. The image is drawn…
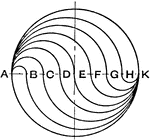
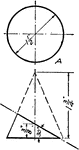
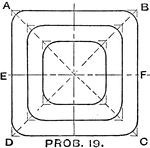
Mechanical Drawing Exercise Three Inscribed Squares with Rounded Corners using Triangle and Bow
"With a 45 degree triangle draw lines AC and BD through the center and construct three squares. Set…
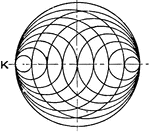
Mechanical Drawing Exercise Shading Sides of Inscribed Circle with Ink
A mechanical drawing practice problem of shading the sides of the inscribed circles. The darker area…
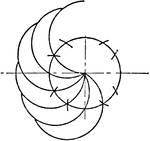
Mechanical Drawing Exercise Shading Sides of Small Circles with Bow Pen
An exercise to shade small circles with bow pen for mechanical drawing. The paper is first divided into…
Mechanical Drawing Exercise Shading Sides of Inscribed Squares and Circle with Ink
Mechanical drawing exercise of shading squares and circle in ink. The squares are first drawn with the…
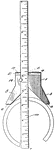
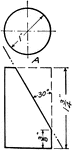
Circular Body Measure Tool
This is a tool used to measure circular bodies, very similar to how current calipers work. This tool…
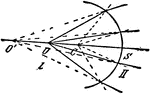
Virtual Image Formed on Spherical Surface
"O' is the virtual image of O formed at a spherical surface of centre C and radius CS." —Encyclopaedia…
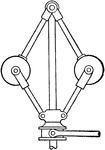
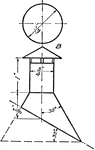
Governor with the Balls Connected to the Base for Steam Engine
A spindle governor where both balls are connected to the base. The governor is used to regulate the…

Shaft in an Eccentric Motion from Steam Engine
"As the eccentric turns in the strap, the point O moves in the dotted circle around O', and the point…
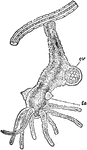
Freshwater Polyp
"Hydra viridis, the freshwater polyp. The animal is attached to the stem of a plant, and is represented…

The Sphere of the Sky
"One standing at O will only see the half of the Sky which is above the circle NESW. The whole sky will…

A Babylonian Map of the World
"A tablet of dark brown clay, much injured, dating from the 8th or 7th century B.C. The two large concentric…

Flanch Shield
"The Flanch is formed of a segment of a circle placed on the side of the shield. It is always borne…

Rustre Shield
"The Rustre differs from the mascle in that the perforation of the device is circular and not throughout."—Aveling,…