Conic Axes
Conjugate diameters perpendicular to each other are called, axes, and the points where they cut the…
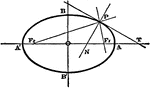
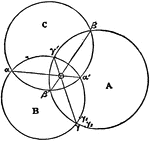
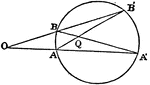
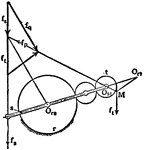
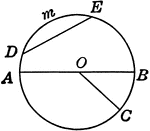
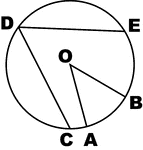
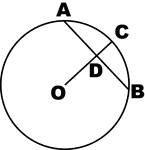
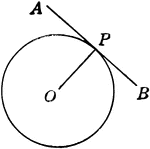
Conic Foci Involution
The lines joining any point on a conic to the two foci are equally inclined to the tangent and normal…
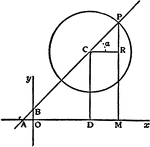
Straight Line
The straight line is the simplest type of locus and the simplest first degree equation.
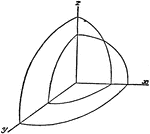
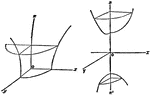
Octant of Wave Surface
the octant of the wave surface cuts each coordinate plane in a circle and an ellipse.
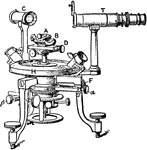
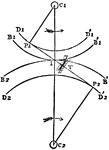
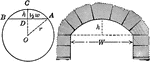
Horizontal-Circle Goniometer
The goniometer is an instrument for measuring the angles of crystals. Nicolaus Stena in 1669 determined…
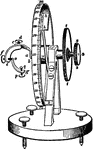
Vertical Circle Goniometer
The goniometer is an instrument for measuring the angles of crystals. Nicolaus Stena in 1669 determined…
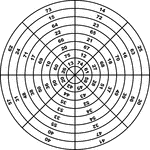
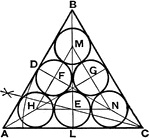
Magic Circle of Circles
The magic circle of circles, first developed by Benjamin Franklin, consists of eight annular rings and…

Gyroscope
Three suspended concentric circles free to move independently of each other at right angles.
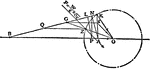
Connecting Rod of a Steam Engine
This illustrates how to determine the force required to turn a connecting rod of a steam engine.
Drawing Lines 4
Circles should be unshaded or shaded evenly with thick and thin lines, changing at about 45 degrees.
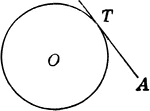
Circle to Circle Tangents
Equal circles inside and tangent to the outside circle, also tangent to each other
Conic Sections 2D
Two dimensional view of the cuts required to create the conic sections hyperbola, parabola, ellipse,…
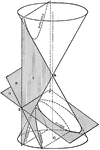
Conic Sections 3D
Three dimensional representation of the intersecting planes required to create the conic sections hyperbola,…
Shaft lining
"Until hard rock is reached the sides of the excavation are supported temporarily by a lining"—Finley,…
Shaft lining
"Until hard rock is reached the sides of the excavation are supported temporarily by a lining"—Finley,…
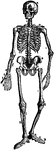
The Human Skeleton
The Human Skeleton. Labels: a, parietal bone; b, frontal; c, cervical vertebrae; d, sternum; e, lumbar…
The Human Ulna and Radius
The Ulna and Radius. Labels: 1, radius; 2, ulna; o, olecranon process, on the anterior surface of which…
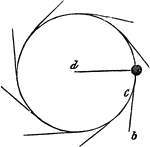
Centrifugal Force
"Suppose a cannon ball, tied with a string to the centre of a slab of smooth marble, and suppose an…
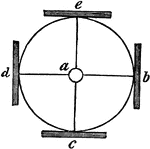
Sound Reflection in a Circle
"In a circle, sound is reflected from every plane surface placed around it, and hence, if the sound…
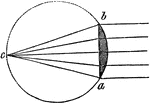
Plano Convex Lens
"If the whole circle be considered the circumfrence of a sphere, of which the plano-convex lens b, a,…
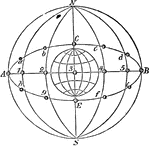
Suns in the Equator and Ecliptic
"Were the Earth's orbit a perfect circle, and her axis perpendicular to the plane of this orbit, the…
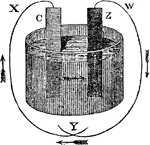
Galvanic Battery
"If we take for example, a slip of zinc, and another of copper, and place the in a cup of diluted sulphuric…
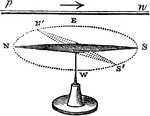
Uniting Wire above the Needle
"The instant this is done and the galvanic circle completed, the needle will deviate from its north…

Section Across the Forearm
A section across the forearm a short distance below the elbow-joint. R and U, its two supporting bones,…
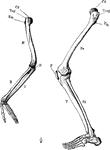
Arm and Leg Skeleton
The skeleton of the arm and leg. Labels: H, the humerus; Cd, its articular head which fits into the…
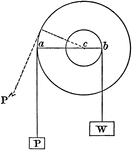
Wheel and Axle
"Considered as a lever, the fulcrum is at the common axis, while the arms of the lever are the radii…

Screw with Lever Arm
"The power is generally applied by a wheel or a lever, and moves through the circumfrence of a circle.…
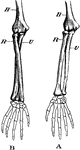
Arm Bones
Demonstration of the movement of a pivot joint. Labels: A, arm in supination (palm uppermost); B, arm…

Cone
"A cone is a solid whose base is a circle and whose convex surface tapers uniformly to a point." —Hallock…

Centrifugal Force
"If a body be fastened to a string and whirled, so as to give it a circular motion, there will be a…
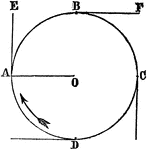
Centrifugal Force
"Attach a ball, for instance, to a cord; and , fastening the end of the cord at a point, O, give a quick…

Centrifugal Force
"The instant one of the strings is let go, the centrifugal force carries off the stone in a tangent…
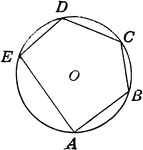
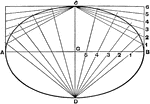
Polygon Inscribed in Circle
Illustration of polygon inscribed in circle. Or, circle circumscribed about the polygon.
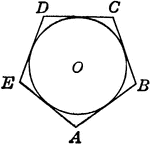
Polygon Circumscribed About Circle
Illustration of polygon circumscribed about circle. Or, circle inscribed in the polygon.

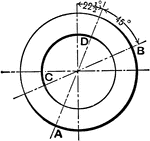
Inscribed and Central Angles 30 60
Illustration of circle with inscribed angle 30 and central angle 60.
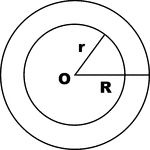
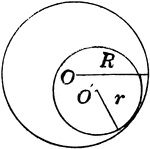
Concentric Circles (Ring) Area
Illustration of concentric circles used to find area between two circles (ring).