Compressed Air Manometer
"The compressed air manometer consists of a strong graduated glass tube of uniform narrow bore, closed…

Primitive Crystal
"In this the four lateral planes are rectangular and equal; they may be either oblong or square; in…
Primitive Crystal
"When the base is a rhomboid, and the prism stands erect, it is only the opposite laeral faces that…
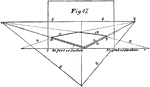
Angular Perspective
The perspective in this plate is "angular perspective," and the figure it represents is a flat square…
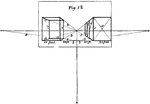
Parallel Perspective
Two upright oblong figures are here represented in parallel perspective. They may be imagined to resemble…

Angular Perspective
This object is a cube, having therefore all its faces of equal dimensions; and as both sides recede,…
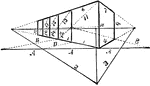
Angular Perspective
This cube has four additional cubes of equal dimensions. This is effected by first drawing the cube…
Filiform antenna
Thread like antenna when the joints are nearly even throughout, cylindrical, tolerably equal in length,…

Great Circle
A Great Circle is one which would be formed on the earth's surface by a plane passing through the earth's…

Small Circle
A small circle is one formed by a plane which does not cut the earth into two equal parts. The small…

Meridians and Parallels
The Meridian of any given place is that half of the meridian circle which passes through that place…

Foraminifera
These animalcule are so small that 1,000,000 are equal in bulk to only one cubic inch. They appear to…

Bread Fruit
Bread-Fruit is the pulpy fruit of a tree which grows only in the tropics. The tree yields fruit during…

Seals and Walrus
Fur Seals make up one of the two distinct groups of mammals called "seals". Both the fur seals and the…

Phylloxera Vastatr
Phylloxera Vastatrix- a, an unaffected rootlet of grape; b, rootlets with newly-formed galls; c, same,…
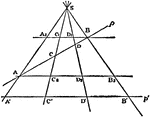
Cross-Ratio Four Points
The cross-ratio of four points in a line is equal to the cross-ratio of their projections on any other…
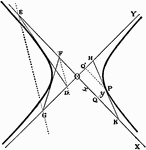
Hyperbola Tangent Triangles
All triangles formed by a tangent and the asymptotes of an hyperbola are equal in area.
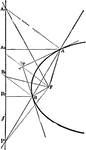
Parabola Foci Properties
The segments between the point of intersection of two tangents to a conic and their points of contact…
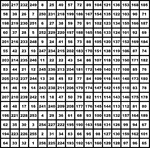
Magic Square
A square divided into equal squares, like a chessboard, in each of which is placed one of a series of…
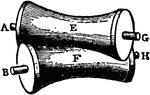
Lateral Sliding Contact
The lines of contact are equal, but the axes are neither parallel to each other, or the line of contact.
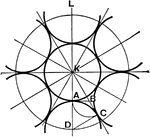
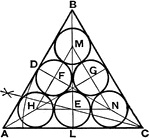
Circle to Circle Tangents
Equal circles inside and tangent to the outside circle, also tangent to each other
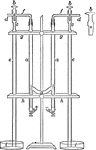
Electrolysis of Hydrochloric Acid
"Hydrochloric acid...is placed in the tubes a. The threeway stopcocks b are turned so that there is…
Combinational Volume
"Suppose our volume of hydrogen to unite with the volume of chlorine; if one particle of hydrogen combines…
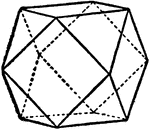
Cubo-octahedron
Represents the combination of a cube and an octahedron, with both faces being equal.
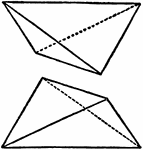
Tetragonal Bishenoids
"This is a double wedge-shaped solid bounded by four equal isosceles triangles." -The Encyclopedia Britannica…
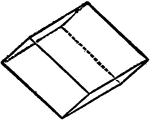
Direct Rhombohedra
"...consisting of six rhomb-shaped faces with the edges all of the equal lengths: the faces are perpendicular…
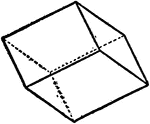
Indirect Rhombohedra
"...consisting of six rhomb-shaped faces with the edges all of the equal lengths: the faces are perpendicular…

Lines of Force under Induction
"Lines of force of a charged sphere and a conductor under induction. The negative electrification on…
Parallel Connection
"Diagram of a multiple or parallel connection. When connected in this manner the voltage of the battery…
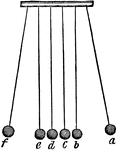
Action and Reaction
"This will be understood, when we consider that the reaction of b is just equal to the action of a,…

Reflected Motion
"Suppose a, b, to be a marble floor, and c, to be an ivory ball, which has be thrown towards the floor…

Center of Gravity
"In a body of equal thickness, as a board, or a slab of marble, but otherwise of an irregular shape,…
Simple Lever System
"Suppose the weight, B to be sixteen pounds and suppose the fulrum to be placed so near it, as to be…
White's Pulley
"In order that the successive wheels should revolve in the same time, and their circumfrences should…
Water Pressure
"Therefore, the small quantity in the spout balances the large quantity in the pot, or presses with…
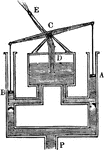
Fire Engine
"The fire engine is a modification of the forcing pump. It consists of two such pumps, the pistons of…
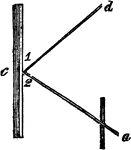
Reflecion of Light
"Let a ray pass towards a mirror in the line a, c, it will be reflected off in the direction of c, d,…
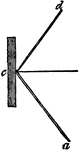
Reflection of Light
"The ray a, c, is the ray of incidence, and that from c, to d, is the ray or reflection. The angles…
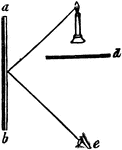
Plane Mirror
"Suppose the mirror, a b, to be placed on the side of a room, and a lamp to be set in antoher room,…
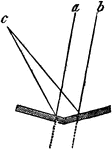
Plane Inclined Mirrors
"The incident rays, a and b, being parallel before they reach the reflectors, are thrown off at unequal…

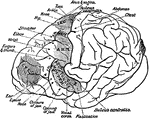
Base of the Skull
The base of the skull. "The lower jaw has been removed. At the lower part of the figure is the hard…

Velocities of Falling Bodies
"When a feather and a cent are dropped from the same height, the cent reaches jthe ground first. this…
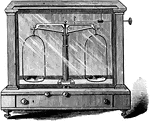
Balance
"The balance is essentially a lever of the first class, having equal arms. The beam carries a pan at…

Wheel and Axle with Rope and Bucket
"...the mechanical advantage of this machine (wheel and axle) equal the ratio between the radii, diameters,…

Pascal's Law
"Pressure exerted anywhere upon a liquid inclosed in a vessel is transmitted undiminished in all direction,…
!["Get a lamp-chimney, preferably cylindrical. With a diamond or a steel glass-cutter, cut a disk of window glass a little larger than the cross-section of the lamp-chimney. Pour some fine emery powder on the disk, and rub one end of the chimney upon it, thus grinding them until they fit accurately...place [the chimney] under the water as shown. the upward pressure of the water will hold the disk in place. Pour water carefully into the tube; the disk will fall as soon as the weight of the water in the chimney plus the weight of th disk, exceeds the upward pressure of the water." -Avery 1895](https://etc.usf.edu/clipart/35900/35965/water_press_35965_mth.gif)
Water Pressure Experiment
"Get a lamp-chimney, preferably cylindrical. With a diamond or a steel glass-cutter, cut a disk of window…

Archimedies Principle
"It is evident that, when a solid is immersed in a fluid, it will displace exactly its own volume of…
Waves with Different Amplitudes with Equal Periods
"...represents two sets of sound waves with like periods and phases but different amplitudes." -Avery…
Waves with Equal Periods and Opposite Amplitudes
"...represents two wave systems of equal periods and amplitudes but of opposite phases." -Avery 1895

Reflected Light
"The apparatus shown is used to prove that incident rays and reflected rays are equal." -Avery 1895
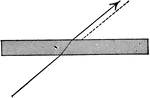
Refraction by Plates
"When radiant energy passes through a medium bounded by parallel planes, the refractions at the two…

Solenoid
"Coil some No. 12 copper wire throuh holes in a board, as shown, and pass a strong current through it.…

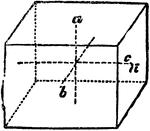
Cube
"A cube is a prism whose faces are ends are squares. All the faces of a cube are equal." —Hallock…

Archimedes Principle
"From on pan suspend a hollow cylinder of metal t, and below that a solid cylinder a of the same size…
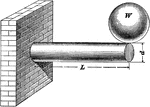
Cylindrical Cantilever
"The maximum safe load in pounds that should be allowed at the end of any cylindrical cantilever is…