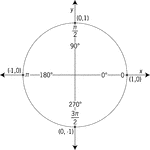
Unit Circle Labeled With Quadrantal Angles And Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
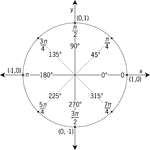
Unit Circle Labeled In 45° Increments With Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
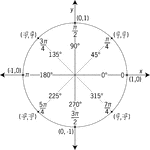
Unit Circle Labeled In 45° Increments With Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
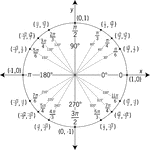
Unit Circle Labeled With Special Angles And Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
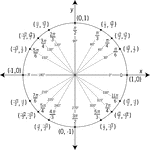
Unit Circle Labeled With Special Angles And Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
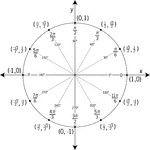
Unit Circle Labeled In 30° Increments With Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
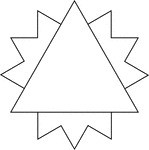
Triangle Inscribed In A 12-Point Star
Illustration of an equilateral triangle inscribed in a closed concave geometric figure with 24 sides…
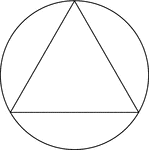
Triangle Inscribed In A Circle
Illustration of an equilateral triangle inscribed in a circle. This can also be described as a circle…
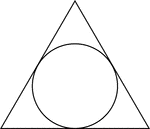
Triangle Circumscribed About A Circle
Illustration of an equilateral triangle circumscribed about a circle. This can also be described as…
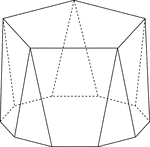
Polyhedron With Pentagon Bases
Illustration of a pentagonal polyhedron that is formed by having two parallel congruent pentagonal bases…

Polyhedron With Pentagon Bases
Illustration of a pentagonal polyhedron that is formed by having two parallel congruent pentagonal bases…
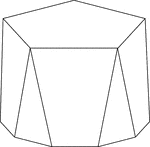
Polyhedron With Pentagon Bases
Illustration of a pentagonal polyhedron that is formed by having two parallel congruent pentagonal bases…
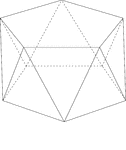
Pentagonal Antiprism
Illustration of a pentagonal antiprism. An antiprism is formed by having two parallel congruent bases…
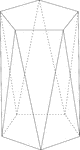
Pentagonal Antiprism
Illustration of a pentagonal antiprism. An antiprism is formed by having two parallel congruent bases…
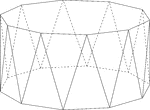
Decagonal Antiprism
Illustration of a decagonal antiprism. An antiprism is formed by having two parallel congruent bases…
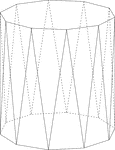
Decagonal Antiprism
Illustration of a decagonal antiprism. An antiprism is formed by having two parallel congruent bases…
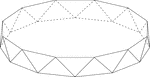
Dodecagonal Antiprism
Illustration of a dodecagonal antiprism. An antiprism is formed by having two parallel congruent bases…
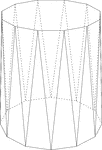
Dodecagonal Antiprism
Illustration of a dodecagonal antiprism. An antiprism is formed by having two parallel congruent bases…
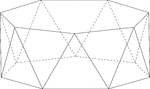
Heptagonal/Septagonal Antiprism
Illustration of a heptagonal, or sometimes known as a septagonal antiprism. An antiprism is formed by…
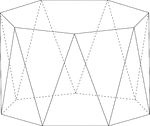
Heptagonal/Septagonal Antiprism
Illustration of a heptagonal, or sometimes known as a septagonal antiprism. An antiprism is formed by…
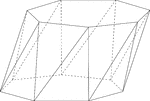
Skewed Heptagonal/Septagonal Antiprism
Illustration of a skewed (non-right) heptagonal, or sometimes known as a septagonal antiprism. An antiprism…
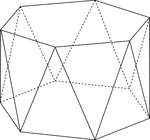
Hexagonal Antiprism
Illustration of a hexagonal antiprism. An antiprism is formed by having two parallel congruent bases…
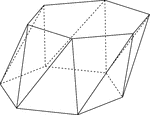
Skewed Hexagonal Antiprism
Illustration of a skewed (non-right) hexagonal antiprism. An antiprism is formed by having two parallel…
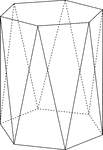
Hexagonal Antiprism
Illustration of a hexagonal antiprism. An antiprism is formed by having two parallel congruent bases…
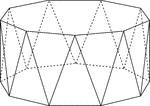
Nonagonal Antiprism
Illustration of a nonagonal antiprism. An antiprism is formed by having two parallel congruent bases…
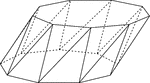
Skewed Nonagonal Antiprism
Illustration of a skewed (non-right) nonagonal antiprism. An antiprism is formed by having two parallel…

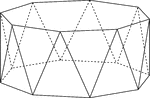
Nonagonal Antiprism
Illustration of a nonagonal antiprism. An antiprism is formed by having two parallel congruent bases…
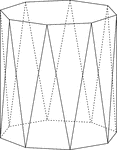
Octagonal Antiprism
Illustration of an octagonal antiprism. An antiprism is formed by having two parallel congruent bases…
Octagonal Antiprism
Illustration of an octagonal antiprism. An antiprism is formed by having two parallel congruent bases…
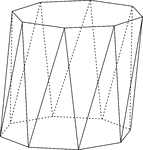
Skewed Octagonal Antiprism
Illustration of a skewed (non-right) octagonal antiprism. An antiprism is formed by having two parallel…
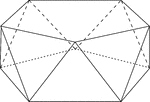
Pentagonal Antiprism
Illustration of a pentagonal antiprism. An antiprism is formed by having two parallel congruent bases…
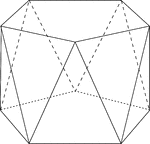
Pentagonal Antiprism
Illustration of a pentagonal antiprism. An antiprism is formed by having two parallel congruent bases…
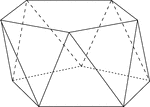
Skewed Pentagonal Antiprism
Illustration of a skewed (non-right) pentagonal antiprism. An antiprism is formed by having two parallel…
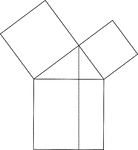
Euclid's Pythagorean Theorem Proof
Illustration used to prove the Pythagorean Theorem, according to Euclid. A perpendicular is drawn from…
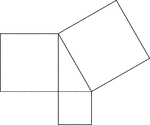
Geometric Pythagorean Theorem Proof
Illustration that can be used to prove the Pythagorean Theorem, the sum of the squares of the legs is…
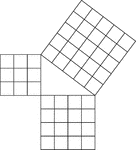
Geometric Pythagorean Theorem Proof
Illustration that can be used to prove the Pythagorean Theorem, the sum of the squares of the legs is…
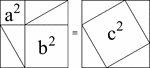
Pythagorean Theorem Proof by Rearrangement
A visual illustration used to prove the Pythagorean Theorem by rearrangement. When the 4 identical triangles…
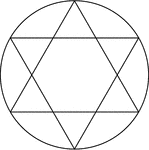
Star Inscribed In A Circle
Illustration of a 6-point star created by two equilateral triangles (often described as the Star of…

Triangle With Circle Constructions
Illustration of a triangle with its incircle and three excircles constructed.
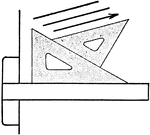
45 Degree Triangle
Triangles are made of various substances such as wood, rubber, celluloid, and steel.
30-60 Degree Triangle
Triangles are made of various substances such as wood, rubber, celluloid, and steel.
Triangle Scales
The triangle scale has six surfaces for different graduations, and the scales are arranged so that the…
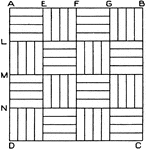
Square Exercise
Square pattern exercise: Divide A D and A B into 4 equal parts and draw horizontal and vertical lines.…
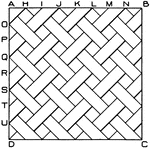
Weave Exercise
Weave pattern exercise: Divide A D and A B into 8 equal parts, and through the points O, P, Q, H, I,…

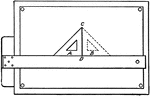
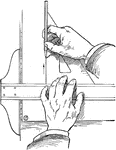
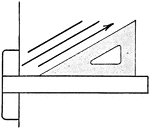
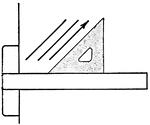
Drawing Parallel Lines Exercise
Parallel lines are drawn by using a triangle in combination with a T-square. To draw a line parallel…
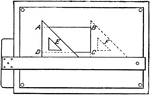
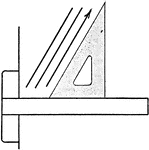
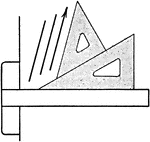
Drawing Perpendicular Lines Exercise
Lines perpendicular to each other may be drawn by using a triangle in combination with the T-square.…
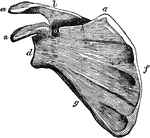
Scapula
Scapula. Labels: a, superior angle; d, the glenoid cavity, or socket for the round head of the arm bone;…

Chest Weights
A man exercising with chest weights. In this position, he extends his left arm out upward at a 45 degree…
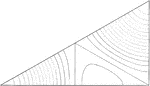
Tide Theory, Triangle
The figure shows a 30 degree triangle made from a square depicting the harmony and syzygy of tides in…

Tide Theory, Triangle
The figure shows a 30 degree triangle made from a square depicting the harmony and syzygy of tides in…