Construction Of Angle On Straight Line
Illustration used to show how to "draw a straight line through any given point on a given straight line…

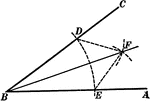
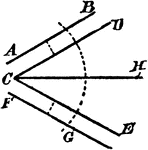
Construction Of A Divided Angle
An illustration showing the construction used to divide an angle into two equal parts. "With C as a…
Construction Of A Divided Angle
An illustration showing the construction used to divide an angle into two equal parts when the lines…
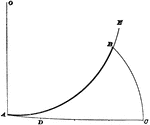
Construction Of Arc
Illustration used to show how to "find an arc of a circle having a known radius, which shall be equal…
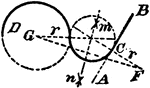
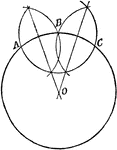
Construction Of A Center And Radius Of A Circle That Will Tangent A Given Circle And Line
An illustration showing how to construct the center and radius of a circle that will tangent a given…
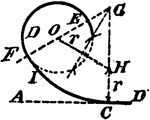
Construction Of A Center And Radius Of A Circle That Will Tangent A Given Circle And Line
An illustration showing how to construct the center and radius of a circle that will tangent a given…
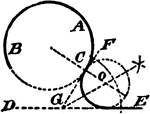
Construction Of A Center And Radius Of A Circle That Will Tangent A Given Circle
An illustration showing how to construct the center and radius of a circle that will tangent a given…
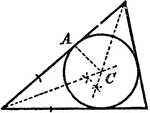
Construction Of The Center And Radius Of A Circle Tangent To Triangle Sides
An illustration showing how to construct a center and radius of a circle that will tangent the three…
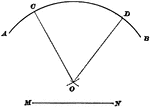
Construction Of Center
Illustration used to show how to find the center when given an arc and its radius.
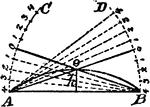
Construction Of A Circle Arc
An illustration showing how to construct a circle arc without recourse to its center, but its chord…
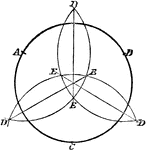
Construction of Circle Given 3 Points
Illustration used to construct a circle when given three points.
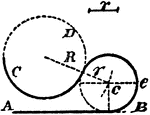
Construction Of A Circle Tangent To A Line And A Circle
An illustration showing how to construct a circle tangent to a given line and given circle. "Add the…
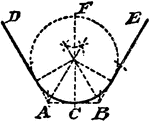
Construction Of A Circle That Tangents 2 Given Lines And Goes Through A Given Point
An illustration showing how to construct a circle that tangents two given lines and goes through a given…
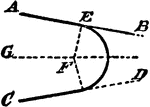
Construction Of A Circle That Tangents 2 Given Lines
An illustration showing how to construct a circle that tangents two given lines inclined to one another…
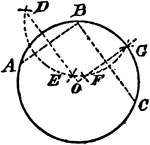
Find The Center Of A Circle Through 3 Points
An illustration showing how to find the center of a circle which will pass through three given points…

Construction Of Circumference
Illustration used to show how to pass a circumference through any three points not in the same straight…
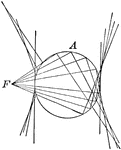
Construction of a Conic
Diagram showing how to construct a conic when given the focus and the auxiliary circle. If the focus…

Focus In Auxiliary Circle of Conic
Diagram showing how to construct a conic when given the focus and the auxiliary circle. The focus is…
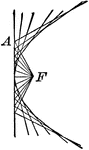
Focus In Auxiliary Circle of Conic
Diagram showing how to construct a conic when given the focus and the auxiliary circle. As the focus…
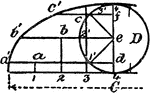
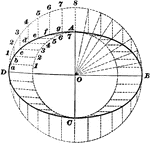
Construction Of A Cycloid
An illustration showing how to construct a cycloid. "The circumference C=3.14D. Divide the rolling circle…
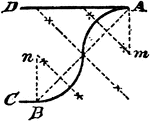
Construction Of A Cyma
An illustration showing how to construct a cyma, or two circle arcs that will tangent themselves, and…

Construction Used to Divide a Line Into Equal Parts
Illustration used to show how to divide a line into any number of equal parts by construction.
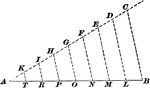
Construction Of Dividing A Line
Illustration used to show how to divide a given straight line into required number of equal parts.
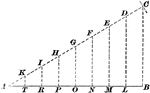
Construction Of Dividing A Line
Illustration used to show how to divide a given straight line into required number of equal parts.

Pattern for Dodecahedron
Pattern that can be cut out and folded to construct a regular dodecahedron. Fold on the dotted lines,…

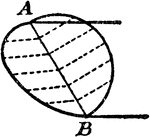
Construction of Ellipse by Describing Circles
Illustration used to draw a an ellipse using string and pins by describing a circles with diameters…
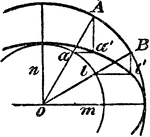
Construction Of An Ellipse Tangent To Two Parallel Lines
An illustration showing how to construct an ellipse parallel to two parallel lines A and B. "Draw a…

Construction of an Ellipse
Illustration of half of an ellipse and its auxiliary circle used to construct an ellipse by points,…
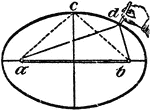
Construction Of An Ellipse
An illustration showing how to construct an ellipse. "With a as a center, draw two concentric circles…
Construction Of An Ellipse
An illustration showing how to construct an ellipse using a string. "Having given the two axes, set…
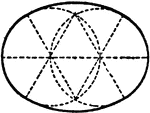
Construction Of An Ellipse
An illustration showing how to construct an ellipse using circle arcs. "Divide the long axis into three…
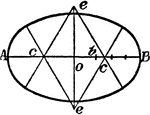
Construction Of An Ellipse
An illustration showing how to construct an ellipse using circle arcs. "Given the two axes, set off…
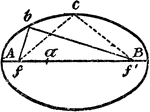
Construction Of An Ellipse
An illustration showing how to construct an ellipse. Given the two axes, set off half the long axis…
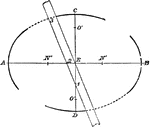
Construction of Ellipse
Illustration used to draw a an ellipse with major axis AB and minor axis CD.
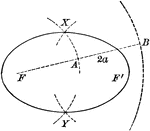
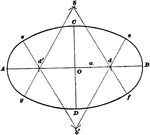
Construction of an Ellipse
Diagram showing how to construct an ellipse when given the two foci and the length of the major axis…
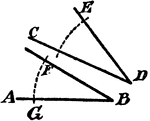
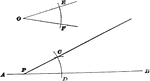
Construction Of An Equal Angle
An illustration showing the construction used to erect an equal angle. "With D as a center, draw the…

Construction Of An Equilateral Triangle Inscribed In A Circle
An illustration showing how to construct an equilateral triangle inscribed in a circle. "With the radius…
Construction Of Equilateral Triangle
Illustration used to show how to draw an equilateral triangle when given one side.
Construction Of Equilateral Triangle
Illustration used to show how to draw an equilateral triangle when given the altitude.

Construction Of An Evolute Of A Circle
An illustration showing how to construct an evolute of a circle. "Given the pitch p, the angle v, and…
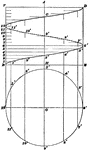
Construction Of Helix
Illustration used to show how to draw a helix when the pitch and the diameter are given.
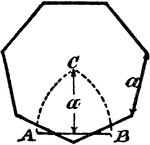
Construction Of A Heptagon
An illustration showing how to construct a heptagon, or septagon. "The appotem a in a hexagon is the…
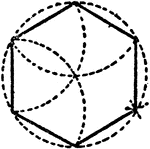
Construction Of A Hexagon In A Circle
An illustration showing how to construct a hexagon in a given circle. "The radius of the circle is equal…
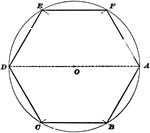
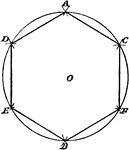
Construction Of Hexagon Inscribed In Circle
Illustration used to show how to inscribe a regular hexagon in a given circle.
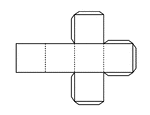
Pattern for Hexahedron
Pattern that can be cut out and folded to construct a regular hexahedron. Fold on the dotted lines,…
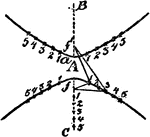
Construction Of A Hyperbola
An illustration showing how to construct a hyperbola by plotting. "Having given the transverse axis…
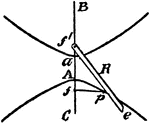
Construction Of A Hyperbola
An illustration showing how to construct a hyperbola by a pencil and a string. "Having given the transverse…
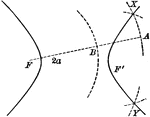
Construction of a Hyperbola
Diagram showing how to construct a hyperbola when given the two foci and the length of the major axis…

Pattern for Icosahedron
Pattern that can be cut out and folded to construct a regular icosahedron. Fold on the dotted lines,…
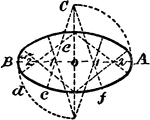
Construction Of An Isometric Ellipse
An illustration showing how to construct an isometric ellipse by compass and six circle arcs. "Divide…
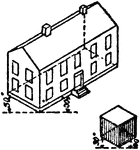
Construction Using Isometric Perspective
An illustration showing how to use isometric perspective. "This kind of perspective admits of scale…
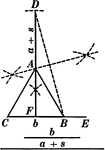
Construction Of An Isosceles Triangle
Illustration of the construction used to create an isosceles triangle, given the bases and the sum of…