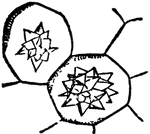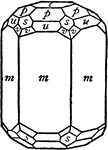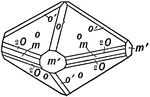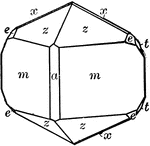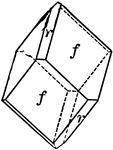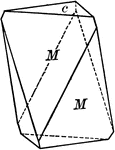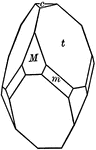
Acanthite
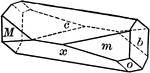
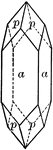
This figure, representing Acanthite, an orthrohombic crystal, shows a combination of the following forms:…
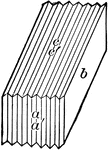
Albite
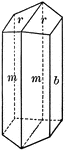
"Triclinic. Twinning very common, according to the albite law and evidenced by fine striation lines…

Ammonium Chloride
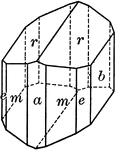
The form 3O3, {311} on Ammonium Chloride (Sal Ammoniac) may have only six of its twenty-four planes…
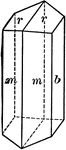
Amphibole
"Monoclinic. Crystals prismatic in habit; the prism faces make angles of 55 and 125 degrees with each…
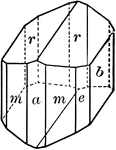
Amphibole
"Monoclinic. Crystals prismatic in habit; the prism faces make angles of 55 and 125 degrees with each…
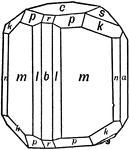
Andalusite
This figure reproduces a combination of orthorhombic forms observed on crystals of aluminum orthosilicate,…
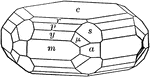
Apatite
"A complex crystal of apatite with the faces of a third-order pyramid upon it." — Ford, 1912
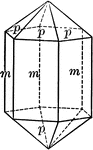
Apatite
"Hexagonal; tri-pyramidal. Crystals usually long prismatic in habit; sometimes short prismatic or tabular.…
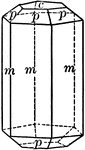
Apatite
"Hexagonal; tri-pyramidal. Crystals usually long prismatic in habit; sometimes short prismatic or tabular.…
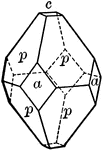
Apophyllite
"Tetragonal. Usually shows a combination of prism of second order, pyramid of first and basal plane."…
Aragonite
"Orthorhombic. Acicular pyramidal; consisting of a prism terminated by a combination of a very steep…
Aragonite
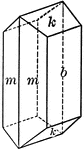
"Orthorhombic. Tabular; consisting of prominent brachypinacoid faces modified by a prism and a low brachydome."…
Arsenopyrite
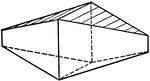
"Orthohombric. Usually in tabular diamond-shaped crystals, formed by a short prism terminated by low…
Arsenopyrite
"Orthohombric. Usually in tabular diamond-shaped crystals, formed by a short prism terminated by low…
Arsenopyrite
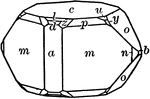
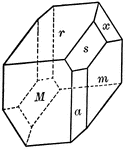
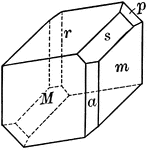
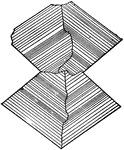
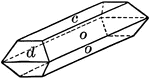
Iron Sulpharsenide (Arsenopyrite), bounded by ∞P, {110} (M), and 1/3P∞̆, {013} (r), forms penetration…
Barite
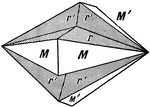
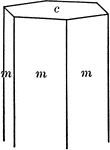
"Orthohombic. Crystals usually tabular parallel to base; often diamond shaped because of the presence…
Barite
"Orthohombic. Crystals usually tabular parallel to base; often diamond shaped because of the presence…

Barium Nitrate
This form shows a crystal of Barium Nitrate exhibiting isometric tetartohedral crystallization.
Beryl
"Hexagonal. Strong prismatic habit. Frequently vertically striated and grooved. Forms usually present…
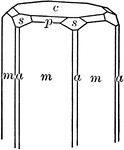
Beryl
"Hexagonal. Strong prismatic habit. Frequently vertically striated and grooved. Forms usually present…
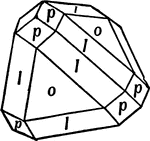
Beveled Tetrahedron
This form shows a tetrahedron (o) with its edges beveled by the trigonal tristetrahedron (l), and its…
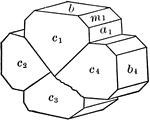
Bournonite
"Orthohombric. Crystals usually short prismatic to tabular. Sometimes quite complex with many prism,…
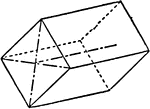
Brachy-prism and Macro-pinacoid
"This consists of four faces perpendicular to the vertical axis." -The Encyclopedia Britannica 1910
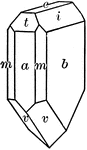
Calamine
"The only orthorhombic mineral of importance belonging to the hemimorphic class is calamine. When its…
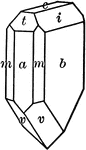
Calamine
"Orthohombic, hemimorphic. Crystals usually tabular parallel to the brachypinacoid. They show prism…
Calc-spar
"Calc-spar occurs at a Scottish locality in acicular pyramidal crystals of which the length may be ten…
Calc-spar
"Calc-spar occurs at a Scottish locality in acicular pyramidal crystals." —The Encyclopedia Britannica,…

Calc-spar
"Calc-spar occurs at a Scottish locality in acicular pyramidal crystals." —The Encyclopedia Britannica,…
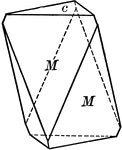
Calcite
"Hexagonal-rhombohedral. Crystals are very varied in habitat, often highly complex. Over 300 different…
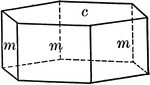
Calcite
"Hexagonal-rhombohedral. Crystals are very varied in habitat, often highly complex. Over 300 different…
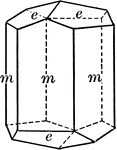
Calcite
"Hexagonal-rhombohedral. Crystals are very varied in habitat, often highly complex. Over 300 different…
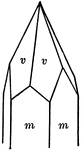
Calcite
"Hexagonal-rhombohedral. Crystals are very varied in habitat, often highly complex. Over 300 different…
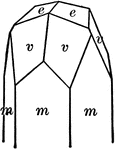
Calcite
"Hexagonal-rhombohedral. Crystals are very varied in habitat, often highly complex. Over 300 different…