Torch
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
Torch
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
Torch
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…

Torch
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…

Torch
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
Torch
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
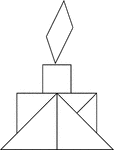
Torch
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…

Tourmaline
"Tourmaline crystals show the forms of the Rhombohedral Class but with hemispherical development. They…
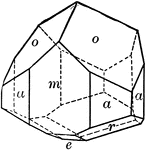
Tourmaline
"Tourmaline crystals show the forms of the Rhombohedral Class but with hemispherical development. They…
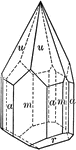
Tourmaline
"Tourmaline crystals show the forms of the Rhombohedral Class but with hemispherical development. They…
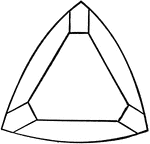
Tourmaline
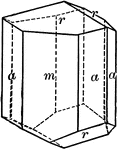
"Hexagonal-rhombohedral; hemimorphic. Crystals usually prismatic, vertically striated. A triangular…
Tourmaline
"Hexagonal-rhombohedral; hemimorphic. Crystals usually prismatic, vertically striated. A triangular…
Parallel Lines Cut By A Transversal Theorem
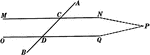
Illustration used to prove the theorem, "If two straight lines are cut by a transversal making a pair…
Parallel Lines Cut By A Transversal Theorem
Illustration used to prove the theorem, "If two parallel lines are cut by a transversal, the alternate…
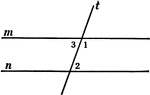
2 Lines Cut By A Transversal
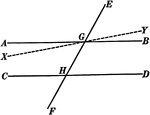
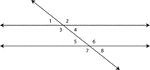
Illustration of two straight lines cut by a transversal. The 8 angles formed are labeled.
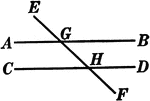
2 Lines Cut By A Transversal
Illustration of two straight lines, AB and CD, cut by a transversal EF.
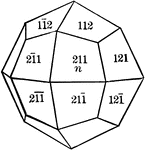
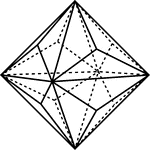
Trapezohedron
"The trapezohedron is a form composed of twenty-four trapezium-shaped faces, each of which intersects…
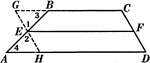
Line Bisecting Trapezoid Sides
Illustration used to prove the theorem "The line bisecting one of the non parallel sides of a trapezoid…

Tree
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
Tree
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…

Tree
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
Tree
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…

Triangle with Church
An illustration of a triangle comprised of a church and two lines. This illustration can be used to…
Triangle with Lighthouse
An illustration of a three triangles created with boats and a lighthouse. This is an example illustration…

Triangle with Tower
An illustration of a triangle comprised of a tower and two lines. This illustration can be used to determine…
Triangle with Tree
An illustration of a triangle comprised of a tree and two lines. This is an example of a problem that…
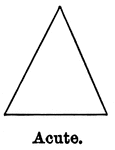
Acute Triangle
Illustration showing an acute triangle (one that has all three angles that are acute).

Angle Bisectors In A Triangle
Illustration used to prove "The bisectors of the angles of a triangle are concurrent in a point which…
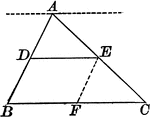
Triangle With Bisector Parallel to the Base
Illustration of a triangle showing that when a line parallel to the base of a triangle bisects one side,…
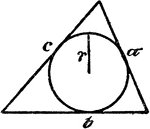
Circle Inscribed In A Triangle
An illustration showing a circle with radius r inscribed in a triangle with sides a, b, and c.
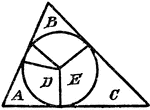
Circle Inscribed In A Triangle
An illustration showing a circle with sectors D and E inscribed in a triangle with angles, A, B, and…
Construction Used to Circumscribe a Circle About a Triangle
Illustration used to circumscribe a circle about a given triangle.

Construction Used to Escribe a Circle to a Triangle
Illustration used to escribe a circle to a given triangle. "A circle which is tangent to one side of…
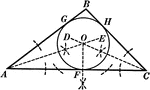
Construction Used to Inscribe a Circle in a Triangle
Illustration used to inscribe a circle in a given triangle.
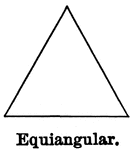
Equiangular Triangle
Illustration showing an equiangular triangle (one that has all three angles that are equal).
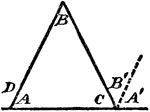
Exterior And Interior Angles Of A Triangle
An illustration showing a triangle with interior angles A, B, C, and exterior angles D, and A' + B'.
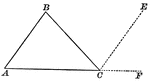
Triangle with Exterior Angles Drawn
Illustration showing a triangle with exterior angles. This can be used to show the sum of the three…
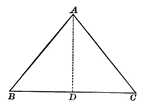
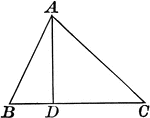
Isosceles Triangle With Interior Segment Drawn
Illustration showing an isosceles triangle with a segment inside. This can be used to show that in an…
Medians In A Triangle
Illustration used to show "Any two medians of a triangle intersect each other in a trisection point…
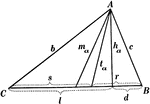
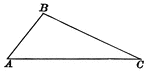
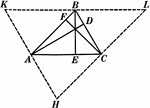
Parts Of A Triangle
Illustration used to show the various parts of a triangle: sides, angles, medians, altitudes, bisectors,…
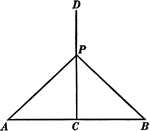
Triangle With Perpendicular Bisector
Illustration showing a perpendicular bisector of a triangle extended outside of the triangle.
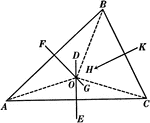
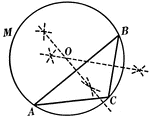
Perpendicular Bisectors In A Triangle
Illustration used to prove "The perpendicular bisectors of the sides of a triangle are concurrent in…
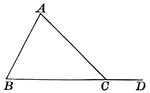
Triangle With Segment Extended for Exterior Angle
Illustration showing a triangle with an exterior segment drawn to show and exterior angle. This can…
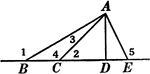
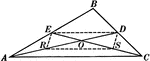
Segments and Angles in a Triangle
Illustration of a triangle with interior segments and angles labeled.
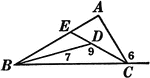
Segments and Angles in a Triangle
Illustration of a triangle with interior segments and angles labeled.
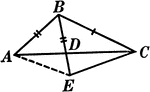
Segments Labeled In A Triangle
Illustration of triangle ABC with BE extended through the triangle at point D. Segment AB is equal to…
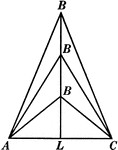
3 Isosceles Triangles Wit Equal Bases
Illustration of three isosceles triangles with the same base AC but varying heights (as B gets farther…