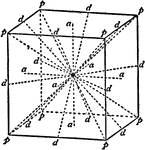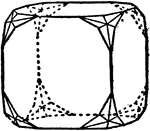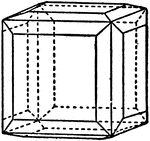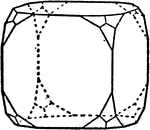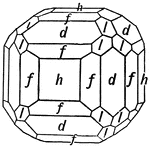
Amalgam
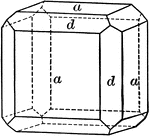
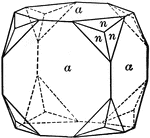
This form shows the cube (h), the dodecahedron (d), the tetrahexahedron (f), and the icositetrahedron…

Children Looking at a Large Box
An illustration of two children, one standing and one resting on its knees, looking at an intricately…
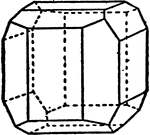
Combination of Pentagonal Dodecahedron and Cube
Represents a combination of a pentagonal dodecahedron and cube, and are common in pyrites.
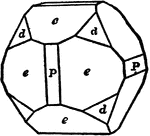
Combination of Pentagonal Dodecahedron, Cube and Octahedron
Represents the combination of pentagonal dodecahedron, cube, and octahedron.

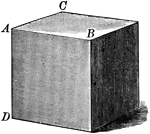
Cube
"Science has succeeded in classifying the thousands of known crystals in six systems, to each of which…

Cube
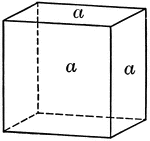
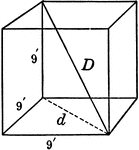
"A cube is a prism whose faces are ends are squares. All the faces of a cube are equal." —Hallock…
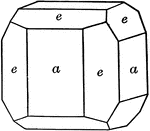
Cube and pyritohedron
"A combination of cube and pyritohedron, in which it will be noted that the faces of the pyritohedron…

Cube and tetrahedron
"A combination of cube and tetrahedron. It will be noted that the tetrahedron faces truncate the alternate…
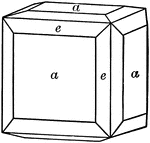
Cube and tetrahexahedron
"A cube with its edges beveled by the faces of a tetrahexahedron." — Ford, 1912

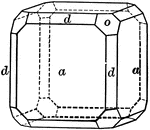
Cube with Additions 1
A cube (A) has sides of 20 inches in length each, making its solid contents equal 8000 cubic inches.…

Cube with Additions 2
In order to fill in the spaces from the three 2000 cubic inch additions, four new additions must be…

Cube with Additions 3
This is the final form of the original 20x20x20 inch or 8000 cubic inch cube with the addition of 7625…
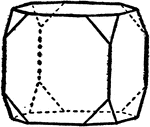
Cube in Combination with Octahedron
Represents the combination of an octrahedron and a cube, with the cube faces predominate.
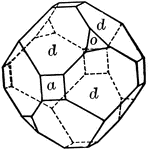
Cube, dodecahedron and tetrahedron
"A combination of cube, dodecahedron, and tetrahedron." — Ford, 1912
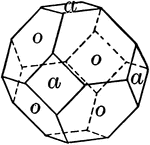
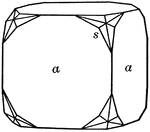
Octahedron trunctuated by cube
"When a corner or an edge of one form is replaced by a face of another form, the first is said to be…

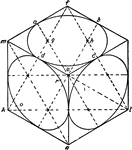
Cube for Illustrating Volume
An illustration of a cube divided into 6 equal pyramids to illustrate how volume can be found.
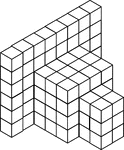
108 Stacked Congruent Cubes
Illustration of 108 congruent cubes stacked at various heights. A 3-dimensional representation on a…
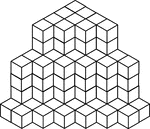
117 Stacked Congruent Cubes
Illustration of 117 congruent cubes stacked in columns of one, four, and six. A 3-dimensional representation…
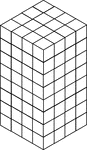
128 Stacked Congruent Cubes
Illustration of 128 congruent cubes stacked so they form a rectangular solid that measures 4 by 4 by…
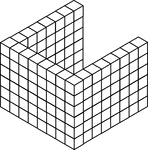
132 Stacked Congruent Cubes
Illustration of 132 congruent cubes stacked in 22 columns of 6 in the shape of a U. A 3-dimensional…
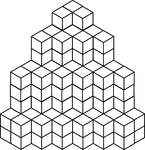
154 Stacked Congruent Cubes
Illustration of 154 congruent cubes stacked in columns increasing from one to four. A 3-dimensional…
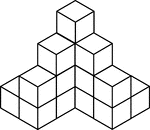
16 Stacked Congruent Cubes
Illustration of 16 congruent cubes stacked at various heights. A 3-dimensional representation on a 2-dimensional…

17 Stacked Congruent Cubes
Illustration of 17 congruent cubes stacked in ones and twos in the shape of a V. A 3-dimensional representation…
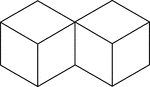
2 Congruent Cubes
Illustration of two congruent cubes that are tangent along an edge. A 3-dimensional representation on…
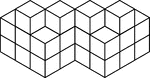
20 Stacked Congruent Cubes
Illustration of 20 congruent cubes stacked in twos and threes. A 3-dimensional representation on a 2-dimensional…
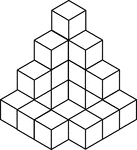
20 Stacked Congruent Cubes
Illustration of 20 congruent cubes stacked at various heights. A 3-dimensional representation on a 2-dimensional…
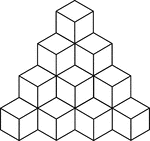
20 Stacked Congruent Cubes
Illustration of 20 congruent cubes stacked at heights increasing from 1 to 4 cubes. A 3-dimensional…
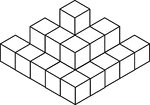
22 Stacked Congruent Cubes
Illustration of 22 congruent cubes stacked in ones, twos, and threes. A 3-dimensional representation…
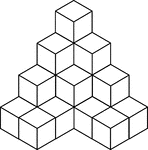
22 Stacked Congruent Cubes
Illustration of 22 congruent cubes stacked at various heights. A 3-dimensional representation on a 2-dimensional…
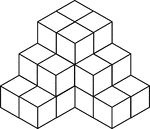
24 Stacked Congruent Cubes
Illustration of 24 congruent cubes stacked at various heights to resemble steps. A 3-dimensional representation…
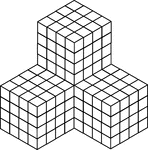
256 Stacked Congruent Cubes
Illustration of 256 congruent cubes stacked so they form 4 larger cubes that measures 4 by 4 by 4 each.…

27 Stacked Congruent Cubes
Illustration of 27 congruent cubes stacked to resemble a larger cube that measures three by three by…
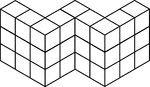
27 Stacked Congruent Cubes
Illustration of 27 congruent cubes stacked at various heights in the shape of a W. A 3-dimensional representation…
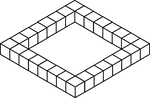
28 Congruent Cubes Placed in the Shape of a Square
Illustration of 28 congruent cubes placed in the shape of a square. A 3-dimensional representation on…