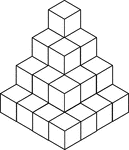
30 Stacked Congruent Cubes
Illustration of 30 congruent cubes stacked in decreasing heights. A 3-dimensional representation on…

33 Stacked Congruent Cubes
Illustration of 33 congruent cubes stacked at various heights in a zigzag pattern. A 3-dimensional representation…
35 Stacked Congruent Cubes
Illustration of 35 congruent cubes stacked in ones and twos in the shape of a W. A 3-dimensional representation…
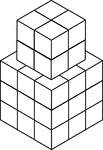
35 Stacked Congruent Cubes
Illustration of 35 congruent cubes stacked at various heights. A 3-dimensional representation on a 2-dimensional…
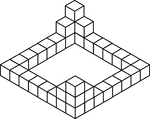
36 Stacked Congruent Cubes
Illustration of 36 congruent cubes stacked at various heights with outer edges forming a square. A 3-dimensional…

36 Stacked Congruent Cubes
Illustration of 36 congruent cubes stacked to resemble a 1 by 1 by 1 cube on a 2 by 2 by 2 cube on a…

39 Stacked Congruent Cubes
Illustration of 39 congruent cubes stacked at various heights. A 3-dimensional representation on a 2-dimensional…

4 Stacked Congruent Cubes
Illustration of 4 congruent cubes stacked in ones and twos. A 3-dimensional representation on a 2-dimensional…
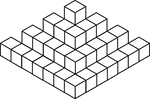
50 Stacked Congruent Cubes
Illustration of 50 congruent cubes stacked at various heights. A 3-dimensional representation on a 2-dimensional…
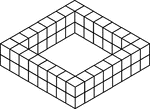
56 Stacked Congruent Cubes
Illustration of 56 congruent cubes stacked in twos in the shape of a square. A 3-dimensional representation…

56 Stacked Congruent Cubes
Illustration of 56 congruent cubes stacked in heights of 1, 4, and 5 cubes that form a zigzag pattern.…
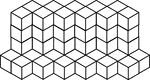
57 Stacked Congruent Cubes
Illustration of 57 congruent cubes stacked in heights of 1 and 5 cubes that form a zigzag pattern. A…
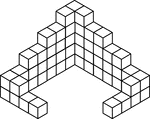
59 Stacked Congruent Cubes
Illustration of 59 congruent cubes stacked at various heights. A 3-dimensional representation on a 2-dimensional…
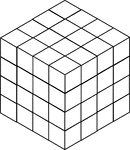
64 Stacked Congruent Cubes
Illustration of 64 congruent cubes stacked so they form a cube that measures 4 by 4 by 4. A 3-dimensional…
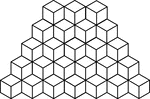
65 Stacked Congruent Cubes
Illustration of 65 congruent cubes stacked at heights increasing from 1 to 5 cubes. A 3-dimensional…
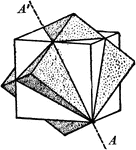
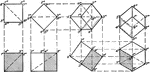
Twinned cubes
"A penetration twin, since the two individuals interpenetrate each other." — Ford, 1912
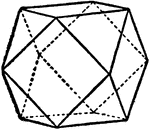
Cubo-octahedron
Represents the combination of a cube and an octahedron, with both faces being equal.
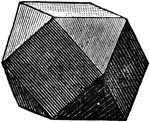
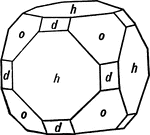
Cuboctahedron
A solid with fourteen faces formed by cutting off the corners of a cube parallel to the coxial octahedron…
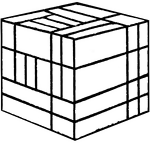
Froebel's Divided Cube (Complex)
This image shows one of Friedrich Froebel's divided cube (this one divided into many smaller cubes and…

Nasik Cube
Squares that have many more summations than just rows, columns, and diagonals. Frost extended this idea…
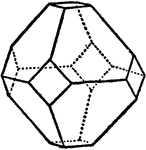
Octahedron in Combination with Cube
Represents the combination of an octahedron and a cube, with the octahedron predominate.

Cube trunctuated by octahedron
"When a corner or an edge of one form is replaced by a face of another form, the first is said to be…

Primitive Crystal
"In this the four lateral planes are rectangular and equal; they may be either oblong or square; in…
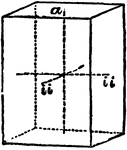
Primitive Crystal
"If the base is a square and the prism stands erect—that is, if its sides or lateral planes, as…
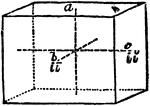
Primitive Crystal
"When the base is a rectangle instead of a square, the form is a right rectangular prism." —The…
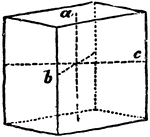
Primitive Crystal
"When the base is a rhombus, and the prism stands erect, the form is a right rhombic prism." —The…
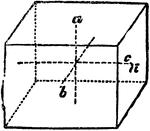
Primitive Crystal
"When the base is a rhomboid, and the prism stands erect, it is only the opposite laeral faces that…