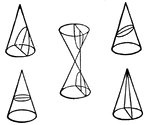
The Cones ClipArt gallery offers 62 examples of three-dimensional geometric solids that are made by taking all straight lines from the apex (top) at an angle to a plane in a 360 degree radius. A cone has a circular base, and looks like a triangle when viewing them from only the x and y axis.
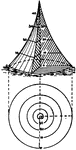
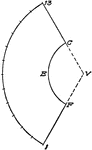
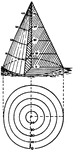
Contours of a concave cone
"The contours of a concave (hollowed out) cone are close together at the center (top), and far apart…
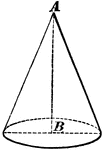
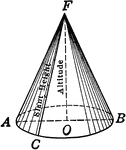
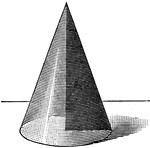
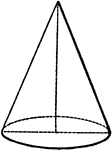
Cone
A cone is a solid whose base is a circle, and whose convex surface tapers uniformly to a point called…
Cone
"If a cone be cut by a plane, parallel to the base, so as to form two parts, the lower part is called…
Cone
"A cone is a solid whose base is a circle and whose convex surface tapers uniformly to a point." —Hallock…
Lateral Area of Cone of Revolution
Illustration of a cone of revolution used to show that the lateral area is equal to half the product…
Contours of a cone
The contours of a cone are circles of different sizes, one within another, and the same distance apart,…
Development Of Cone
Illustration of the development of a cone. When the cone covered in paper (figure a) is rolled out on…
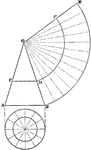
Development Of Cone
Illustration of the development of a cone along a stretchout described with the radius OB.
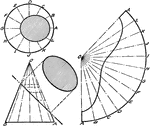
Development of Cone
A rolled out image of a cone by dividing the base in equal parts and arcs to measure the true lengths.
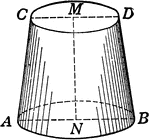
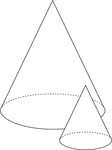
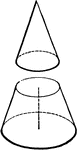
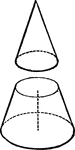
Circular Cone Frustum
An illustration of a circular cone with the top cut off by a plane parallel to the base. The remaining…
Frustum of Cone to Find Lateral Area
"The lateral area of a frustum of a cone of revolution is equal to half the sum of the circumferences…
Frustum of Cone to Find Volume
"The volume of a frustum of a circular cone is equivalent to the sum of the volumes of three cones whose…
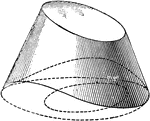
Intersection Of A Plane And Cone
Illustration showing the intersection of a plane with a cone. The solid is shown in perspective and…
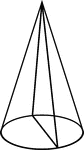
Plane Passing Through A Cone
Illustration showing a cone cut by a plane that is along the axis of symmetry.

Plane Passing Through the Vertex of a Cone
Illustration of a plane passing through the vertex of a cone (section made is a triangle).
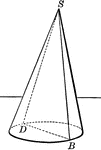
Plane Passing Through the Vertex of a Cone
Illustration of a plane passing through the vertex of a cone (section made is a triangle).
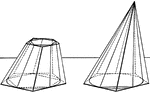
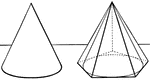
Cone With Regular Polygon Inscribed and Circumscribed About
Illustration of a pyramid and with a regular polygon inscribed in and circumscribed about a cone. "If…
Right Circular Cone
An illustration of a right circular cone with labels on slant height and altitude.
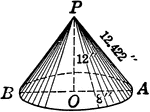
Right Circular Cone
An illustration of a right circular cone with labels on slant height (12.422), radius (8), and altitude…
Right Circular Cone
Illustration of a right circular cone with the diameter of the base equal to the height of the cone.
Right Circular Cone
Illustration of a right circular cone with the diameter of the base greater than the height of the cone.
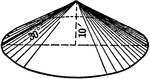
Right Circular Cone 10 Feet High With 30 Degree Angle
An illustration of a right circular cone with altitude of 10 ft. and angle of 30 degrees.
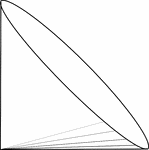
Right Circular Cone on Side
Illustration of a right circular cone resting on an element such that the vertex is on the bottom and…
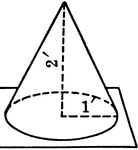
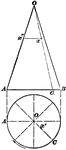
Right Circular Cone With 2 ft. Height and 1 ft. Radius
An illustration of a right circular cone with la radius of 1 foot and a height of 2 feet. Illustration…
Right Circular Cone With Hole Cut Out
An illustration of a right circular cone with labels on dimensions, and hole cut out. Illustration could…

Tangent Plane to a Cone
Illustration of a plane tangent to a cone which contains one element of the cone but does not cut the…
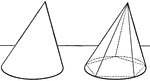
Volume of Cone
Illustration of a cone with a polygon inscribed used to show that the volume of a circular cone is equal…
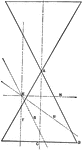
Conic Sections 2D
Two dimensional view of the cuts required to create the conic sections hyperbola, parabola, ellipse,…
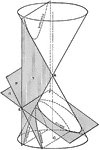
Conic Sections 3D
Three dimensional representation of the intersecting planes required to create the conic sections hyperbola,…
Cone depicting Conic Sections
Diagram of a cone with spheres and cut by a plane to depict the conic sections.
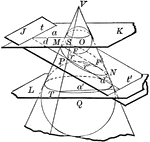
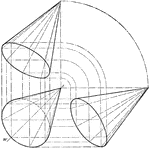
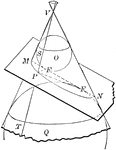
Cone depicting Conic Sections
Diagram of a cone with inscribed spheres and cut by various planes to depict the conic sections: circle,…
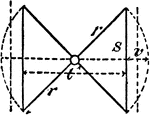
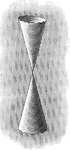
Intersecting Lines Of A Double Cone
An illustration showing a model of intersecting lines that that are formed by a double cone.
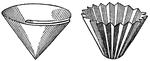
Paper Filter
Paper filter used in chemistry experiments. The filter on the left is folded to fit into a funnel. The…
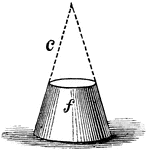
Frustum of a Cone
"The part of any solid between two planes, which may be either parallel or inclined to each other: as,…
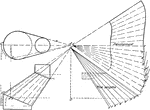
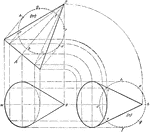
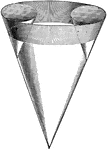
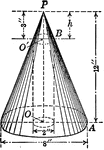
Oblique Cone by Triangulation Connecting to Two Parallel Pipes of Different Diameters
"An oblique cone connecting two parallel pipes of different diameters... the true size of the base is…
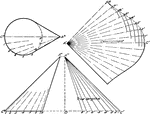
Development of Oblique Cone by Triangulation
A development or rolled out oblique cone using triangulation. The method of triangulation is done by…
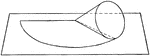
Paint Strainer
This is a paper and cloth intended to be used once or twice and then destroyed to avoid cleaning.