Conic Sections: Hyperbolas
This mathematics ClipArt gallery offers 28 images of conic sections, or conics, creating hyperbolas. Conics are obtained by taking a cone, or conical surface, and intersecting it with a plane. Conic hyperbolas are retrieved by intersecting the cones with a plane, often perpendicular to the circles created by the cones. The result are unbound (meaning not closed shapes) curves that are hyperbolas.
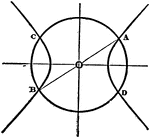
Conic Axes
Conjugate diameters perpendicular to each other are called, axes, and the points where they cut the…
Rolling of Equal Hyperbolas
Illustration of the rolling of equal hyperbolas. If two equal hyperbolas are placed so that the distances…
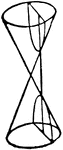
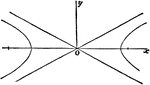
Hyperbola
Illustration showing a hyperbola as a curve formed by the intersection of the surface of a cone with…

Asymptotes of a Hyperbola
Illustration showing the asymptotes of a hyperbola. The asymptotes will never meet the curve.
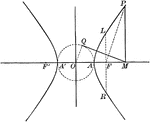
Auxiliary Circle and Hyperbola
Illustration of a hyperbola and its auxiliary circle. "Any ordinate of a hyperbola is to the tangent…
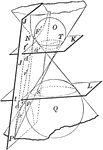
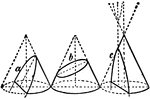
Cone Intersected by a Plane to Form a Hyperbola
Diagram depicting a cone with both nappes intersected by plane J to form a hyperbola.
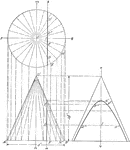
Conic Section Hyperbola
Illustration of a cone cut by a plane parallel to the axis of the cone and perpendicular to the vertical…
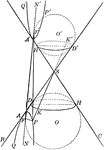
Conic Section Showing an Hyperbola
Illustration showing the definition of an hyperbola as a conic section. "The section of a right circular…
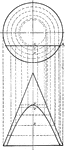
Conic Section Showing Hyperbola
Illustration showing the definition of a hyperbola as a conic section.
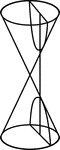
Conic Section Showing A Hyperbola
Illustration showing the definition of an hyperbola as a conic section. A hyperbola is formed from a…
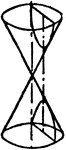
Conic Section Showing A Hyperbola
An illustration showing the intersection of a plane and a double cone. The cone is intersected by a…
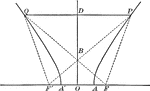
Conjugate Axis of a Hyperbola
Illustration showing how the a hyperbola is symmetrical with respect to its conjugate axis.
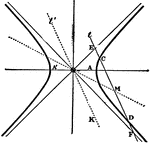
Hyperbola Conjugate Diameters
Any two conjugate diameters of an hyperbola are harmonic conjugates with regard to the asymptotes.
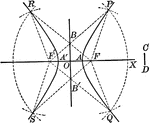
Construction of Hyperbola
Illustration showing how a hyperbola con be constructed by points, having been given the foci and the…
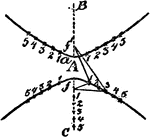
Construction Of A Hyperbola
An illustration showing how to construct a hyperbola by plotting. "Having given the transverse axis…
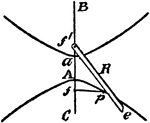
Construction Of A Hyperbola
An illustration showing how to construct a hyperbola by a pencil and a string. "Having given the transverse…
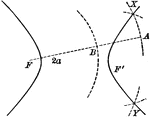
Construction of a Hyperbola
Diagram showing how to construct a hyperbola when given the two foci and the length of the major axis…
Demonstration of Hyperbola Definition
Illustration showing the definition of an hyperbola. "An hyperbola may be described by the continuous…
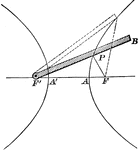
Foci Distance of Hyperbola
Illustration of a hyperbola with distances to foci drawn. "The difference of the distances of any point…
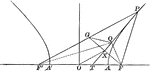
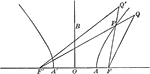
Line Bisecting Angle Between Focal Radii in Hyperbola
Illustration of a hyperbola with a line bisecting the focal radii. "If through a point P of an hyperbola…
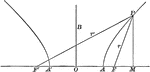
Point on a Hyperbola
Illustration of a point on a hyperbola. "If d denotes the abscissa (x-coordinate) of a point of an hyperbola,…
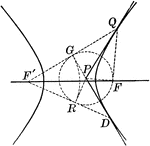
Tangent to Hyperbola
Illustration showing how to draw a tangent to an hyperbola from a given point P on the convex side of…
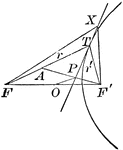
Tangent to a Hyperbola
Diagram part of a hyperbola with a tangent line that illustrates "A line through a point on the hyperbola…
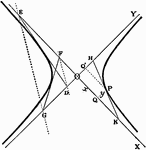
Hyperbola Tangent Triangles
All triangles formed by a tangent and the asymptotes of an hyperbola are equal in area.
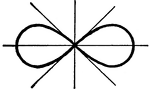
Lemniscate
A Lemniscate is, in general, a curve generated by a point moving so that the product of its distances…
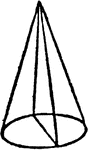
Degenerate Conic Forming Triangle
Illustration showing intersecting straight lines meeting to form a triangle. It is formed by the intersection…