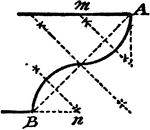
Construction Of A Talon
An illustration showing how to construct a talon, or two circle arcs that will tangent themselves, and…
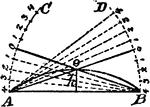
Construction Of A Circle Arc
An illustration showing how to construct a circle arc without recourse to its center, but its chord…
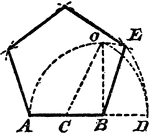
Construction Of A Pentagon On A Line
An illustration showing how to construct a pentagon on a given line without resort to its center. "From…
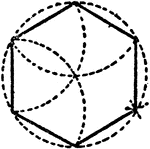
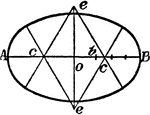
Construction Of A Hexagon In A Circle
An illustration showing how to construct a hexagon in a given circle. "The radius of the circle is equal…
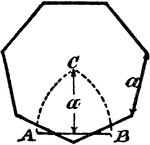
Construction Of A Heptagon
An illustration showing how to construct a heptagon, or septagon. "The appotem a in a hexagon is the…
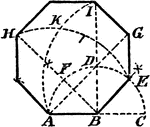
Construction Of An Octagon
An illustration showing how to construct an octagon on a given line. "Prolong AB to C. With B as center…
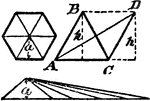
Area Of Regular Polygon Proof
An illustration showing that the area of a regular polygon is equal to the area of a triangle whose…
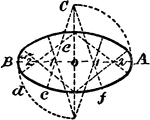
Construction Of An Isometric Ellipse
An illustration showing how to construct an isometric ellipse by compass and six circle arcs. "Divide…
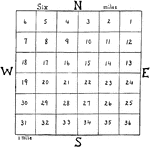
Land Measurement
"A regular township, according to United States surveys, is 6 miles square and is divided into 36 equal…
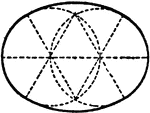
Construction Of An Ellipse
An illustration showing how to construct an ellipse. "With a as a center, draw two concentric circles…
Construction Of An Ellipse
An illustration showing how to construct an ellipse using circle arcs. "Divide the long axis into three…
Construction Of An Ellipse
An illustration showing how to construct an ellipse using circle arcs. "Given the two axes, set off…
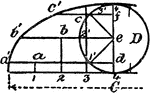
Construction Of An Ellipse Tangent To Two Parallel Lines
An illustration showing how to construct an ellipse parallel to two parallel lines A and B. "Draw a…
Construction Of A Cycloid
An illustration showing how to construct a cycloid. "The circumference C=3.14D. Divide the rolling circle…

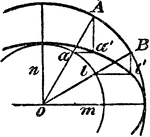
Construction Of An Evolute Of A Circle
An illustration showing how to construct an evolute of a circle. "Given the pitch p, the angle v, and…
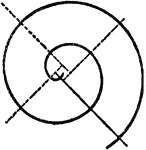
Construction Of A Spiral
An illustration showing how to construct a spiral with compasses and four centers. "Given the pitch…

Construction Of A Parabola
An illustration showing how to construct a parabola. "Given the vertex A, axis x, and a point P. Draw…
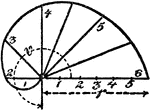
Construction Of An Arithmetic Spiral
An illustration showing how to construct an arithmetic spiral. "Given the pitch p and angle v, divide…

Addition Scale
A balance scale holding 5 pounds on the left and 3 and 2 pound weights on the right showing 3+2=5.
Five Eighths
The shaded region represents 5/8 of the rectangle. If II is divided in to thirds, then those pieces…
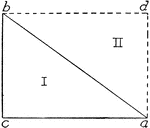
Area of Triangle
"The triangle ABC is divided into 2 right triangles I and II. ABC is seen to be equal to 1/2 of the…
Area of Triangle
"The child sees triangle ACB = triangle ADB, and that I + II = CA - DB; and so he sees that the area…
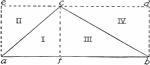
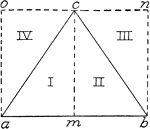
Area of Triangle
"Fig. 3 shows triangle I = triangle II, III = IV, and so triangle ABC = 1/2 of rectangle ABDE. The fact…
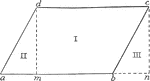
Area of Parallelogram
"From Figure 4 he sees a parallelogram equal to a rectangle of the same base and altitude. Cut out and…
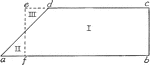
Area of Trapezoid
"The student sees the trapezoid is equal in area to a rectangle whose base is the average base of the…
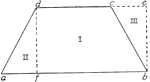
Area of Trapezoid
"The student sees the trapezoid is equal in area to a rectangle whose base is the average base of the…
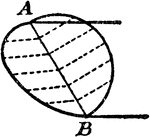
Area of Sphere
"It is found that the cord covering the curved surface is twice as long as the one covering the flat…

Velocities Of Rigidly-connected Points
Illustration for rigidly-connected points. "If two points are so connected that their distance apart…
Diagram of the Nervous System of a Centipede
In the nervous system of the centipede the ganglions are arranged in pairs of nearly equal size, except…
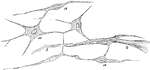
Tissue Growth of the Uterus
In the embryo the place of fibrous tissues is at first occupied by a mass of roundish cells, derived…

Infundibula
Two small infundibula or groups of air cells, a, with air cells, b, and the ultimate bronchial tubes,…

Testis of a Dog, Section of the
From a section of the testis of a dog, showing portions of seminal tubes. A, seminal epithelial cells,…

Lake and Vegetation
"Diagram illustrating the gradual filling up of lakes by the encroachment of vegetation, and also the…
Helix
A cylindrical helix is a curve generated by a point moving uniformly around a cylinder and uniformly…
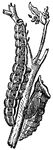
Caterpillar and Chrysalis of Pieris Brassicae
"It lives in groups on cabbages in gardens, and similar vegetables. It is so voracious that it consumes…
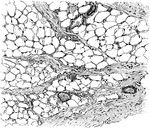
Adipose Tissue from Omentum
Adipose tissue from omentum. The fat cells are arranged as groups between the bundles of connective…
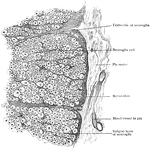
Transverse Section of Spinal Cord
Peripheral part of transverse section of spinal cord, showing nerve fibers subdivided into groups by…
Pulley System
This figure has six pulleys and one cord passes round them all. Each pulley is stretched with the same…
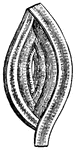
Spiroloculina Depressa
One group will take the spherical form and produce a shell in the shape of the nautilus. Some are more…

Rotalia
One group will take the spherical form and produce a shell in the shape of the nautilus. Some are more…

Backward Movement of Discharging Vessel
This experiment illustrates the law of action and reaction, which asserts that momentum cannot be imparted…

Torricellian Experiment
This experiment showed that every surface exposed to the atmosphere sustains a normal pressure equal…

Counterpoised Barometer
If the barometric tube is suspended from one of the scales of a balance, there will be required to balance…
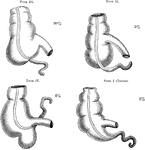
Four Types of Cecum
The four types of cecum. Type I is the infantile form which persists throughout life, in about 2 percent…

Maturation of the Ovum
The maturation of the ovum. A, An ovum at the commencement process. B, After the formation of the spindle.…

Vincent Colyer
Vincent Colyer (1825 - July 12, 1888) was a successful American artist noted for the images he created…

Puritan Costumes
A Puritan of 16th and 17th century England was an associate of any number of religious groups advocating…

A Puritan Soldier
A Puritan of 16th and 17th century England was an associate of any number of religious groups advocating…

Bowery Theater
An illustration of Bowery Theater, a playhouse in the Bowery neighborhood of New York City. Although…
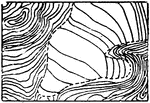
Glacier Contours
In cartography, a contour line (often just called a "contour") joins points of equal elevation (height)…

Glacier Form Lines
In cartography, a contour line (often just called a "contour") joins points of equal elevation (height)…
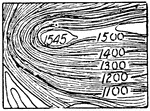
Contour System
In cartography, a contour line (often just called a "contour") joins points of equal elevation (height)…

Guanaco
The guanaco (Lama guanicoe) is a camelid animal native to South America that stands between 107 and…
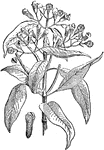
Clove Plant and Seed
Cloves (Syzygium aromaticum, syn. Eugenia aromaticum or Eugenia caryophyllata) are the aromatic dried…

Curassow
Curassows are one of the three major groups of cracid birds. Three of the four genera are restricted…
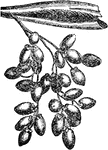
Dates
An illustration of the fruit of a date palm, a date. The fruit is a drupe known as a date. They are…