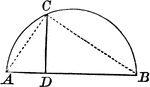
Right Triangle Inscribed in Semicircle Shows Mean Proportional
Right triangle inscribed in semicircle. Illustration shows that the perpendicular from any point in…
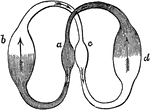
Blood Circulation in the Heart
Diagram showing the circulation of blood in the heart. Let a represent the right side of the…

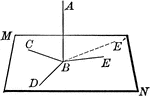
Line Perpendicular to Plane
If a straight line is perpendicular to each of two other straight lines in a plane at their point of…
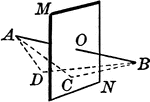
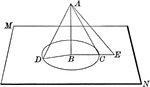
Locus Point to a Plane
"The locus of a point in space equidistant from the extremities of a straight line is the plane perpendicular…
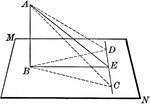
Line Perpendicular to Plane
Straight line AB is perpendicular to the lines in plane MN at point B. "If from the foot of a perpendicular…
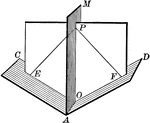
Dihedral Angle With Bisector
Illustration of a dihedral angle bisected by a plane. "Every point in a plane which bisects a dihedral…

Polyhedral Angle
Illustration of polyhedral angle. "The opening of three or more planes which meet at a common point…
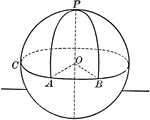
Sphere With Quadrants and Poles
A sphere with quadrants and poles. "A point on the surface of a sphere, which is at the distance of…
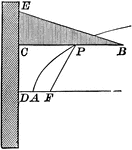
Parabola With Focus and Directrix
Illustration of a parabola - a curve which is the locus of a point that moves in a plane so that its…
Parabola With Focus and Directrix
Illustration of a parabola - a curve which is the locus of a point that moves in a plane so that its…

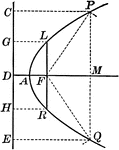
Parabola With Coordinates and Latus Rectum
Illustration of a parabola showing that any point of a parabola is the mean proportional between the…

Point on Parabola
Illustration of a parabola showing point P is equidistant to the focus and the directrix.
Point on Parabola
Illustration of a parabola. "If a line PT is drawn from any point P of the curve, bisecting the angle…

Electric Telephone
"When a person speaks into the transmitter, the pulsations of the air, produced by the voice, produce…
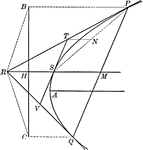
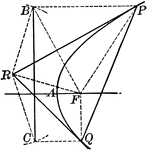
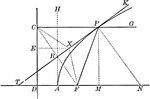
Tangents to a Parabola
Illustration showing that if two tangents RP and RQ are drawn from a point R to a parabola, the line…
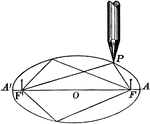
Demonstration of Ellipse Definition
Illustration showing the definition of an ellipse. "An ellipse is a curve which is the locus of a point…
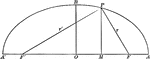
Focal Radii of an Ellipse
Illustration of half of an ellipse. "If d denotes the abscissa of a point of an ellipse, r and r' its…
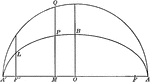
Ordinate and Major Axis of Ellipse
Illustration of half of an ellipse. The square of the ordinate of a point in an ellipse is to the product…
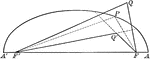
Point Distances to Foci on Ellipse
Illustration of half of an ellipse. "The sum of the distances of any point from the foci of an ellipse…
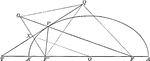
Line Bisecting Angle Between Focal Radii on Ellipse
Illustration of half of an ellipse. "If through a point P of an ellipse a line is drawn bisecting the…
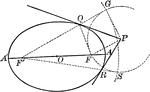
Tangent From External Point to an Ellipse
Illustration of how to draw a tangent to an ellipse from an external point.

Tangents to an Ellipse
Illustration showing the tangents drawn at two corresponding points of an ellipse and its auxiliary…
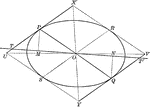
Parallel Tangents to an Ellipse
Illustration showing that tangents drawn at the ends of any diameter are parallel to each other.
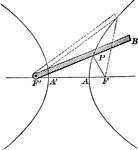
Demonstration of Hyperbola Definition
Illustration showing the definition of an hyperbola. "An hyperbola may be described by the continuous…

Point on a Hyperbola
Illustration of a point on a hyperbola. "If d denotes the abscissa (x-coordinate) of a point of an hyperbola,…
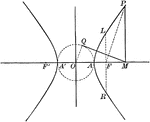
Auxiliary Circle and Hyperbola
Illustration of a hyperbola and its auxiliary circle. "Any ordinate of a hyperbola is to the tangent…
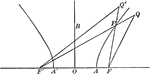
Foci Distance of Hyperbola
Illustration of a hyperbola with distances to foci drawn. "The difference of the distances of any point…
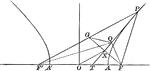
Line Bisecting Angle Between Focal Radii in Hyperbola
Illustration of a hyperbola with a line bisecting the focal radii. "If through a point P of an hyperbola…
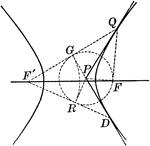
Tangent to Hyperbola
Illustration showing how to draw a tangent to an hyperbola from a given point P on the convex side of…
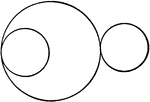
Tangent Circles
Illustration of tangent circles. One circle is said to be tangent to another circle when they touch…

Circle With a Perpendicular Drawn to the Diameter
"If from any point on the circumference of a circle, a perpendicular be let fall upon a given diameter,…
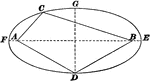
Ellipse
Illustration of an ellipse with major and minor axes, foci, and points on the ellipse. "An ellipse is…

Silver Trime Coin, 1851
Trime (3 cents) United States coin from 1851. Obverse has the Union shield lying on top of a six-pointed…
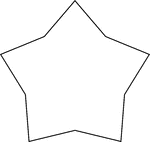
Concave Equilateral Decagon
A 5-point star made from a non-regular concave decagon in which all sides are equal in length.

Concave Equilateral Dodecagon
A 6-point star made from a non-regular concave dodecagon in which all sides are equal in length. There…
Circular Rosette With 6 Petals
Circular rosette with 6 petals in a circle. It is made by rotating circles about a fixed point. The…

Circular Rosette With 12 Petals
Circular rosette with 12 petals in a circle. It is made by rotating circles about a fixed point. The…
Circular Rosette With 24 Petals
Circular rosette with 24 petals in a circle. It is made by rotating circles about a fixed point. The…

Circular Rosette With 48 Petals
Circular rosette with 48 petals in a circle. It is made by rotating circles about a fixed point. The…
Circular Rosette With 4 Petals
Circular rosette with 6 petals in a circle. It is made by rotating circles about a fixed point. The…

Circular Design
Circular design made by rotating circles about a fixed point. The radii of the smaller circles is equal…

Circular Design
Circular design made by rotating circles about a fixed point. The radii of the smaller circles is equal…
Circular Rosette With 8 Petals
Circular rosette with 8 petals in a circle. It is made by rotating circles about a fixed point. The…

Circular Rosette With 16 Petals
Circular rosette with 16 petals in a circle. It is made by rotating circles about a fixed point. The…
Circular Rosette With 32 Petals
Circular rosette with 32 petals in a circle. It is made by rotating circles about a fixed point. The…
Circular Rosette With 8 Petals
Circular rosette with 8 petals in a circle. It is made by rotating circles about a fixed point. The…
Circular Rosette With 16 Petals
Circular rosette with 16 petals in a circle. It is made by rotating circles about a fixed point. The…

Circular Rosette With 32 Petals
Circular rosette with 32 petals in a circle. It is made by rotating circles about a fixed point. The…
5 Tangent Circles
A sequence of five circles tangent to each other at a point. The radius decreases by one half in each…
Reflected Arcs Of 2 Circles In A Circle
A design created by dividing a circle into 4 equal arcs and creating a reflection of each arc toward…
Reflected Arcs Of 2 Circles
A design created by dividing a circle into 4 equal arcs and reflecting each arc toward the center of…
Reflected Arcs Of 2 Circles
A design created by dividing a circle into 4 equal arcs and reflecting each arc toward the center of…

Reflected Arcs Of 4 Circles In A Circle
A design created by dividing a circle into 4 equal arcs and creating a reflection of each arc toward…
Reflected Arcs Of 4 Circles In A Circle
A design created by dividing a circle into 4 equal arcs and creating a reflection of each arc toward…

Reflected Arcs Of 8 Circles In A Circle
A design created by dividing a circle into 4 equal arcs and creating a reflection of each arc toward…