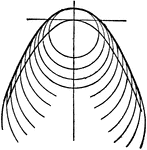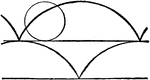
Cycloid
Illustration showing a cycloid curve. "The curve generated by a point in the plane of a circle when…

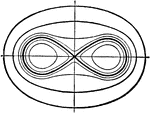
Cycloids
Illustration showing cycloid curves. "The curve generated by a point in the plane of a circle when the…
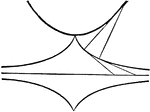
Cycloid
Illustration showing a cycloid curve. "The curve generated by a point in the plane of a circle when…
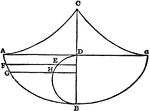
Trajectory
Trajectory is the path a moving object follows through space. A trajectory can be described mathematically…
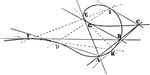
Satellite
"Nodal Cubic, with four primary lines and their satellite. In the diagram, ABC is the satellite line.…
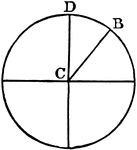
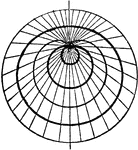
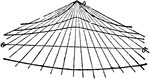
Sector
"In geometry: (a) A plane figure inclosed between the arc of a circle, ellipse, or other central curve…

Refinement
"Architectural Refinement from Church of St. Quentin, France ... deviations from the geometrical…
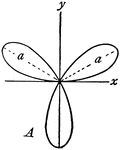
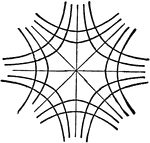
Rose
"In geometry, certain transcendental curves having, in polar coordinates, equations of the form ρ…
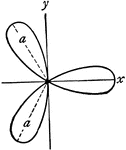
Rose
"In geometry, certain transcendental curves having, in polar coordinates, equations of the form ρ…

Rose
"In geometry, certain transcendental curves having, in polar coordinates, equations of the form ρ…
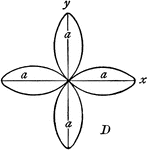
Rose
"In geometry, certain transcendental curves having, in polar coordinates, equations of the form ρ…

Grolier Scroll
"Grolier scroll, the flowing curved lines that surround and interlace the geometrical framework of a…
Eccentric Angle
"In geometry, an angle connected with an ellipse and defined as ... angle BCL, reckoned from one determinate…

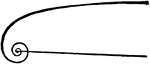
Epicycloid
"In geometry, a curve generated by the motion of a point on the circumference of a circle which rolls…
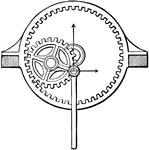
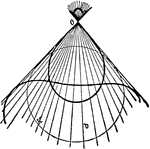
Epicycloidal Wheel
"Epicycloidal wheel, a wheel or ring fixed to a framework, toothed on its inner side, and having in…

Triangle with Tower
An illustration of a triangle comprised of a tower and two lines. This illustration can be used to determine…

Triangle with Church
An illustration of a triangle comprised of a church and two lines. This illustration can be used to…
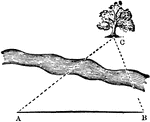
Triangle with Tree
An illustration of a triangle comprised of a tree and two lines. This is an example of a problem that…
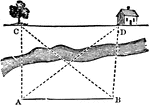
Square
An illustration of a square and triangles within the square. This is an example of a problem that can…
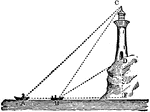
Triangle with Lighthouse
An illustration of a three triangles created with boats and a lighthouse. This is an example illustration…
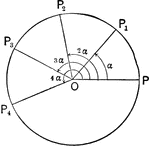
Geometric Inspection of Complex Numbers
Illustration showing complex numbers with a modulus equal to unity. The lines representing these numbers…
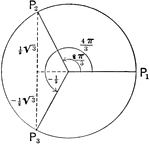
Cubed Roots of Unity
Illustration showing how to find the cubed roots of unity by applying DeMoivre's Theorem.

Fifth Roots of Unity
Illustration showing how to find the fifth roots of unity by applying DeMoivre's Theorem.
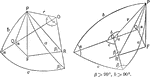
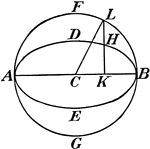
Relationships In A Spherical Triangle
Illustration used, with the law of sines, to find the relation between two sides of a spherical triangle…
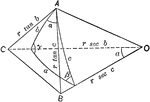
Relationships In A Spherical Triangle
Illustration used, with the law of cosines, to find the relation between the three sides and an angle…
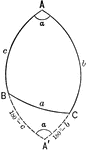
Relationships In A Spherical Triangle
Illustration used to extend the law of cosines when finding the relation between the three sides and…
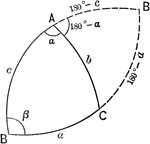
Relationships In A Spherical Triangle
Illustration used to extend the law of cosines when finding the relation between the three sides and…

Right Spherical Triangle
Illustration of a right spherical triangle with a and b the sides, and α and β the angles…
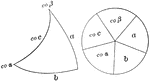
Napier's Right Spherical Triangle
Illustration of a right spherical triangle and the five circular parts placed in the sectors of a circle…

Cube with Additions 1
A cube (A) has sides of 20 inches in length each, making its solid contents equal 8000 cubic inches.…

Cube with Additions 2
In order to fill in the spaces from the three 2000 cubic inch additions, four new additions must be…

Cube with Additions 3
This is the final form of the original 20x20x20 inch or 8000 cubic inch cube with the addition of 7625…

Folium of Descartes
"Folium of Descartes, with its asymptote. The equation is (4-y)(y-1)2 = 3x2y ... In geometry, a plane…
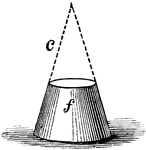
Frustum of a Cone
"The part of any solid between two planes, which may be either parallel or inclined to each other: as,…
Double Arch
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
Arch
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…

Triangular Double Arch
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…

Bear
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…

Camel
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…

Lit Candle
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…

Sitting Cat
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…

Cat
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…

Cormorant
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…

Cup
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…

Dancer
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…

Double Arrow
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…

Diver
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…

Dog
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…