Popcorn Box Frustum Of A Rectangular Pyramid
Popcorn box that is in the shape of a frustum of a rectangular pyramid.
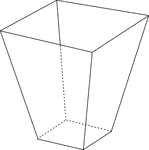
Frustum Of A Rectangular Pyramid
Illustration of a right hollow rectangular pyramid that has been cut by a plane parallel to the base.…
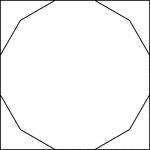
Square Circumscribed About A Dodecagon
Illustration of a square circumscribed about a regular dodecagon. This could also be described as a…
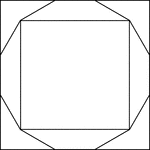
Squares Inscribed and Circumscribed About a Regular Dodecagon
Illustration of 2 squares; one inscribed in a regular dodecagon and the other circumscribed about the…

Square Inscribed In A Dodecagon
Illustration of a square inscribed in an regular dodecagon. This could also be described as a regular…
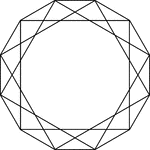
3 Square Inscribed In A Dodecagon
Illustration of 3 squares inscribed in an regular dodecagon. Each vertex of the dodecagon is also a…
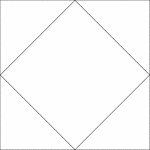
Square Inscribed In A Square
Illustration of a square inscribed in a square. The interior square is rotated 45° in relation to…
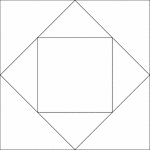
Squares Inscribed In Squares
Illustration of a square inscribed in a square that is inscribed in another square. Each successive…
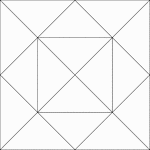
Squares Inscribed In Squares
Illustration of a square inscribed in a square that is inscribed in another square. Each successive…
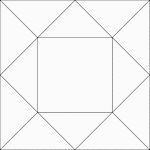
Squares Inscribed In Squares
Illustration of a square inscribed in a square that is inscribed in another square. Each successive…
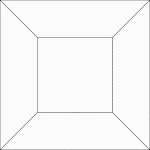
2 Concentric Squares
Illustration of 2 concentric squares whose vertices are connected by line segments.
2 Congruent Rotated Squares
Illustration of 2 congruent squares that have the same center. One square has been rotated 45° in…
4 Congruent Rotated Squares
Illustration of 4 congruent squares that have the same center. Each square has been rotated 22.5°…
8 Congruent Rotated Squares
Illustration of 8 congruent squares that have the same center. Each square has been rotated 11.25°…
16 Congruent Rotated Squares
Illustration of 16 congruent squares that have the same center. Each square has been rotated 5.625°…
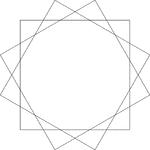
3 Congruent Rotated Squares
Illustration of 3 congruent squares that have the same center. Each square has been rotated 30°…

6 Congruent Rotated Squares
Illustration of 6 congruent squares that have the same center. Each square has been rotated 15°…

12 Congruent Rotated Squares
Illustration of 12 congruent squares that have the same center. Each square has been rotated 7.5°…
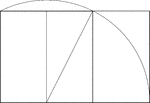
Construction Of A Golden Rectangle
Illustration showing the construction of a golden rectangle. Beginning with a unit square, a line is…

Golden Rectangle
Illustration showing the golden rectangle. Two quantities are considered to be in the golden ratio if…

Golden Rectangles
Illustration showing a nesting of 2 golden rectangles. Two quantities are considered to be in the golden…

Golden Rectangles
Illustration showing a nesting of 3 golden rectangles. Two quantities are considered to be in the golden…

Golden Rectangles
Illustration showing a nesting of 4 golden rectangles. Two quantities are considered to be in the golden…

Golden Rectangles
Illustration showing a nesting of 5 golden rectangles. Two quantities are considered to be in the golden…

Golden Rectangles
Illustration showing a nesting of 6 golden rectangles. Two quantities are considered to be in the golden…
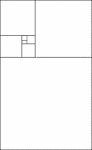
Golden Rectangles
Illustration showing a nesting of 7 golden rectangles. Two quantities are considered to be in the golden…

Golden Rectangles
Illustration showing succession of golden rectangles that are used to construct the golden spiral. Two…

Golden Rectangles
Illustration showing succession of golden rectangles that are used to construct the golden spiral. Two…
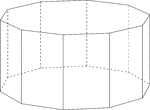
Decagonal Prism
Illustration of a decagonal prism with regular decagons for bases and rectangular faces. The hidden…
Swimming Pool Shaped Like A Decagonal Prism
Illustration of a swimming pool and water hose that is in the shape of a hollow regular decagonal prism…
Star-Shaped Decagonal Prism
Illustration of a non-regular decagonal prism in the shape of a star. Then ends/bases are made of star-shaped…
Star-Shaped Decagonal Prism
Illustration of a non-regular decagonal prism in the shape of a star. Then ends/bases are made of star-shaped…
Star-Shaped Decagonal Prism
Side view of a non-regular decagonal prism in the shape of a star. Then ends/bases are made of star-shaped…
Decagonal Prism
Illustration of a right decagonal prism with regular decagons for bases and rectangular faces.
Similar Decagonal Prisms
Illustration of 2 similar right decagonal prisms. Both have regular decagons for bases and rectangular…
Decagonal Prism Resting On Its Side
Illustration of a right decagonal prism with regular decagons for bases and rectangular faces. The prism…
Heptagonal/Septagonal Prism
Illustration of a hollow right heptagonal/septagonal prism with regular heptagons/septagons for bases…
Heptagonal/Septagonal Prism
Illustration of a regular right heptagonal/septagonal prism with regular heptagons/septagons for bases…
Heptagonal/Septagonal Prism
Illustration of a right heptagonal/septagonal prism with regular heptagons/septagons for bases and rectangular…
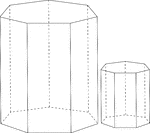
Similar Heptagonal/Septagonal Prisms
Illustration of 2 similar right heptagonal/septagonal prisms. Both have regular heptagons/septagons…
Heptagonal/Septagonal Prism
Illustration of a right heptagonal/septagonal prism with regular heptagons/septagons for bases and rectangular…

Hexagonal Prism
Illustration of a right hexagonal prism with a height less than the length of the edge of the hexagon.

Hexagonal Prism
Illustration of a right hexagonal prism with a height greater than the length of the edge of the hexagon.

Similar Hexagonal Prisms
Illustration of 2 similar right hexagonal prisms. The height of the prism and length of the side of…
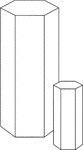
Similar Hexagonal Prisms
Illustration of 2 similar right hexagonal prisms. The height of the prism and length of the side of…
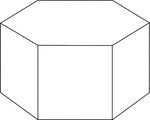
Hexagonal Prism
Illustration of a right hexagonal prism with hexagons for bases and square faces. The hidden edges are…

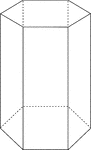
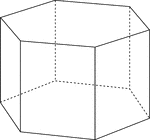
Hexagonal Prism
Illustration of a right hexagonal prism with hexagons for bases and rectangular faces. The height of…
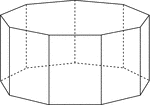
Nonagonal Prism
Illustration of a right nonagonal prism with regular nonagons for bases and rectangular faces. The hidden…
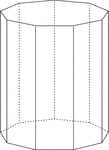
Nonagonal Prism
Illustration of a right nonagonal prism with regular nonagons for bases and rectangular faces. The height…
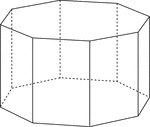
Octagonal Prism
Illustration of a right octagonal prism with regular octagons for bases and rectangular faces. The hidden…
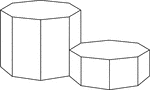
2 Octagonal Prisms
Illustration of 2 right octagonal prisms with congruent bases, but different heights. The height of…
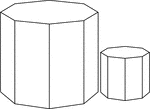
2 Similar Octagonal Prisms
Illustration of 2 Similar right octagonal prisms. The height and length of the edges of the smaller…