Development of Cylinder
A rolled out, or development, of the cylinder. The development is created by drawing the top curve with…
Development of Cone
A development, or rolled out, cone where the point A is the meeting point for the sides. The development…
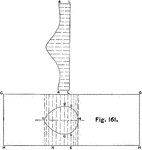
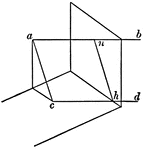
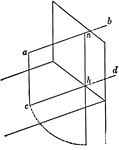
Development of Two Intersecting Cylinder
A development, or rolled out image, of two cylinders intersecting each other. The large rectangular…
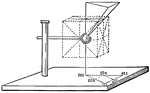
Isometric Holohedral Mirror
This image represents an isometric holohedral mirror positioned to produce a cube by reflection.
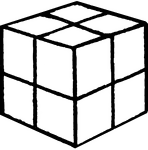
Froebel's Divided Cube (Eight Smaller Cubes)
This image shows one of Friedrich Froebel's divided cube (this one divided into eight smaller cubes).…
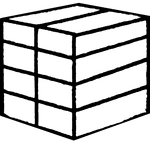
Froebel's Divided Cube (Eight Smaller Parallelograms)
This image shows one of Friedrich Froebel's divided cube (this one divided into eight smaller parallelograms).…

Froebel's Divided Cube (Twenty-seven Smaller Cubes)
This image shows one of Friedrich Froebel's divided cube (this one divided into twenty-seven smaller…
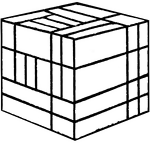
Froebel's Divided Cube (Complex)
This image shows one of Friedrich Froebel's divided cube (this one divided into many smaller cubes and…
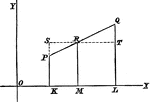
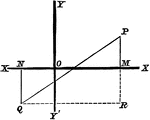
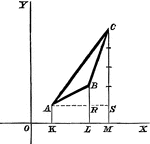
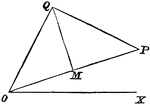
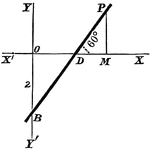
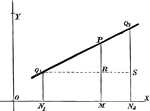
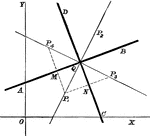
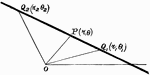
Point Ratio
Showing how to find points on a coordinate plane. Also, shows an example of the midpoint formula.
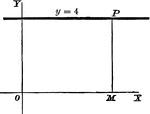
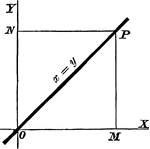
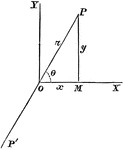
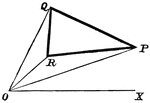
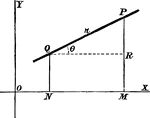
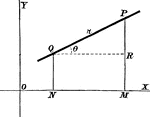
Perpendicular Line
A perpendicular line on a coordinate plane, showing what y the y-coordinate will be.
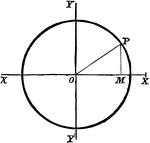
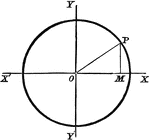
Circle Equation
To find the equation of a circle whose center is the origin and whose radius is 3 units in length.
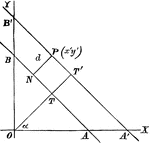
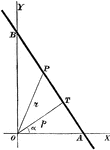
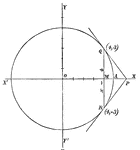
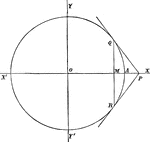
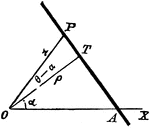
Perpendicular Distance
Finding the perpendicular distance of points whose equation is x cosa + y sina = p.
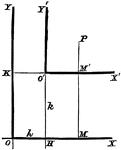
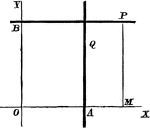
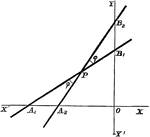
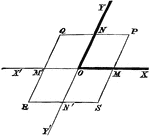
Axes Shift
Any system of coordinate axes to another set which is parallel to the former, but with different origins.
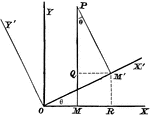
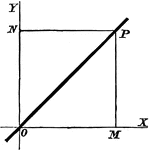
Rectangular Axes
Transforming from one set of rectangular axes to another with the same origin, but different direction.
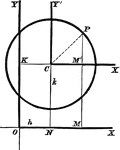
Common Form of Circle
A circle in its common, or central form. This is used to assist students in finding the equation of…
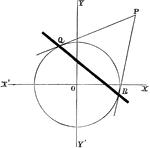
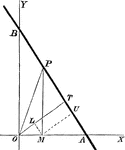
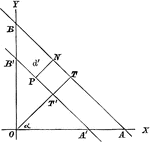
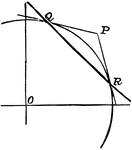
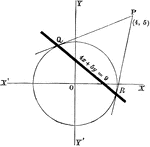
Chord Equation
Tangent lines are drawn from a given external point to a circle. The equation is found by joining their…
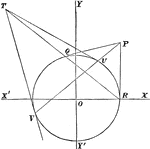
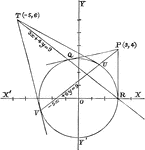
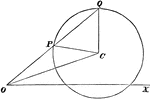
Polar Property
If the chords of a circle are drawn through a fixed point, then the points of intersection of the pairs…
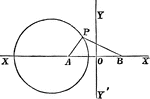
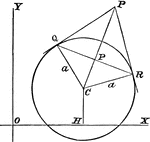
Coordinate Plane
A circle with part of a triangle inscribed in it. They are lying on a coordinate plane.

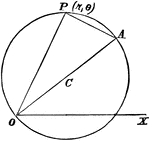
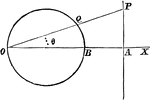
Circle with Secant
A secant is "a line which cuts a figure in any way. Specifically, in trigonometry, a line from the center…

Snowflakes as Described by William Scoresby
"The aqueous vapor of the atmosphere precipitated in a crystalline form, and falling to the earth in…
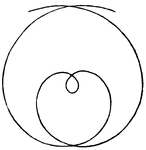
Archimedean Spiral
Illustration of a spiral named after the 3rd century BC Greek mathematician Archimedes.