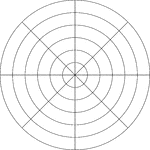
Polar Grid In Degrees With Radius 6
Illustration of a polar graph/grid that is marked, but not labeled, in 45° increments and units…
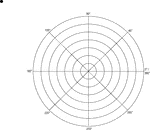
Polar Grid In Degrees With Radius 7
Illustration of a polar graph/grid that is marked and labeled in 45° increments and units marked…
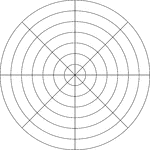
Polar Grid In Degrees With Radius 7
Illustration of a polar graph/grid that is marked, but not labeled, in 45° increments and units…
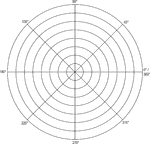
Polar Grid In Degrees With Radius 8
Illustration of a polar graph/grid that is marked and labeled in 45° increments and units marked…
Polar Grid In Degrees With Radius 8
Illustration of a polar graph/grid that is marked, but not labeled, in 45° increments and units…

Polar Grid In Degrees With Radius 9
Illustration of a polar graph/grid that is marked and labeled in 45° increments and units marked…
Polar Grid In Degrees With Radius 9
Illustration of a polar graph/grid that is marked, but not labeled, in 45° increments and units…

3 Ladders Leaning Against a Wall
Illustration of 3 ladders leaning against the side of a building (wall) to form right triangles. The…
Extension Ladder
Illustration of an extension ladder. If ladder is leaned against a building, it will form a right triangle…
Leaning Ladder
Illustration of a ladder that is not perpendicular to the ground. If it is set on the ground and leaned…
Leaning Ladder
Illustration of a ladder that is not perpendicular to the ground. If it is set on the ground and leaned…
Leaning Ladder
Illustration of a ladder that is not perpendicular to the ground. If it is set on the ground and leaned…

Leaning Ladder
Illustration of a ladder that is not perpendicular to the ground. If it is set on the ground and leaned…
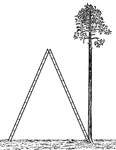
2 Ladders Leaning Against a Tree
Illustration of 2 ladders leaning against opposite sides of a palm tree to form similar right triangles.…

Ladder Leaning Against a Tree
Illustration of a ladder leaning against a palm tree, that is perpendicular to the ground, to form a…

Ladder Leaning Against a Building
Illustration of a ladder leaning against the side of a building (wall) to form a right triangle .
Open Stepladder
Illustration of a stepladder that is opened to form an isosceles triangle with the ground.

Leaning Tower
Illustration of a leaning tower with a perpendicular drawn from the top of the tower to the ground to…

Ladder Leaning Against a Tree
Illustration of a ladder leaning against a palm tree, that is perpendicular to the ground, to form a…
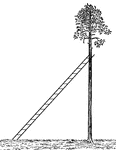
Ladder Leaning Against a Tree
Illustration of a ladder leaning against a palm tree, that is perpendicular to the ground, to form a…
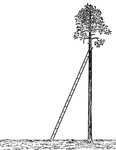
Ladder Leaning Against a Tree
Illustration of a ladder leaning against a palm tree, that is perpendicular to the ground, to form a…
Skyscraper Giant Stepladder
Illustration of a giant stepladder, sometimes called a skyscraper stepladder, that is opened next to…
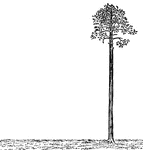
Palm Tree Perpendicular to Ground
Illustration of a palm tree that is perpendicular to the ground. The tree is perfectly straight, as…

Open Stepladder
Illustration of a stepladder that is opened to form an isosceles triangle with the ground.
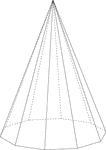
Decagonal Pyramid
Illustration of a right decagonal pyramid. The base is a decagon and the faces are isosceles triangles.…

Inverted Decagonal Pyramid
Illustration of a hollow right decagonal pyramid. The base is a decagon and the faces are isosceles…
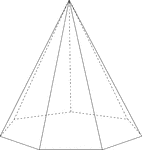
Septagonal/Heptagonal Pyramid
Illustration of a right septagonal/heptagonal pyramid with hidden edges shown. The base is a heptagon…

Inverted Septagonal/Heptagonal Pyramid
Illustration of a hollow right heptagonal (septagonal) pyramid. The base is a heptagon and the faces…
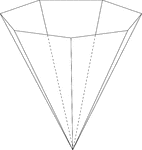
Inverted Septagonal/Heptagonal Pyramid
Illustration of a hollow right heptagonal (septagonal) pyramid. The base is a heptagon and the faces…
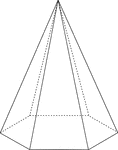
Hexagonal Pyramid
Illustration of a right hexagonal pyramid with hidden edges shown. The base is a hexagon and the faces…
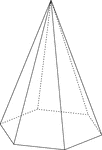
Hexagonal Pyramid
Illustration of a right hexagonal pyramid with hidden edges shown. The base is a hexagon and the faces…
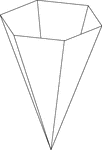
Inverted Hexagonal Pyramid
Illustration of a hollow right hexagonal pyramid. The base is a hexagon and the faces are isosceles…
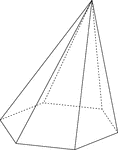
Skewed Hexagonal Pyramid
Illustration of a non-right, or skewed, hexagonal pyramid with hidden edges shown. The base is a hexagon…
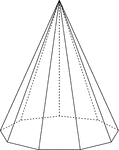
Nonagonal Pyramid
Illustration of a right nonagonal pyramid with hidden edges shown. The base is a nonagon and the faces…
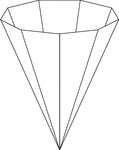
Inverted Nonagonal Pyramid
Illustration of a hollow right nonagonal pyramid. The base is a nonagon and the faces are isosceles…
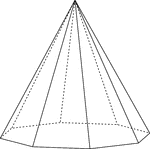
Octagonal Pyramid
Illustration of a right octagonal pyramid with hidden edges shown. The base is an octagon and the faces…
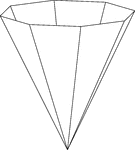
Inverted Octagonal Pyramid
Illustration of a hollow right octagonal pyramid. The base is an octagon and the faces are isosceles…
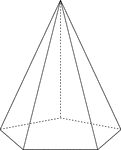
Pentagonal Pyramid
Illustration of a right pentagonal pyramid with hidden edges shown. The base is an pentagon and the…
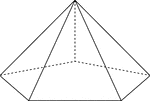
Pentagonal Pyramid
Illustration of a right pentagonal pyramid with hidden edges shown. The base is an pentagon and the…
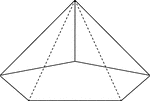
Pentagonal Pyramid
Illustration of a right pentagonal pyramid viewed from below with hidden edges shown. The base is an…
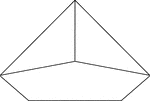
Pentagonal Pyramid
Illustration of a right pentagonal pyramid viewed from below. The base is an pentagon and the faces…
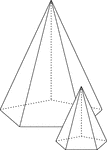
Similar Pentagonal Pyramids
Illustration of 2 similar right pentagonal pyramids with hidden edges shown. The height of the pyramid…
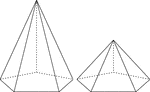
2 Right Pentagonal Pyramids
Illustration of 2 right pentagonal pyramids with hidden edges shown. The pentagonal bases are congruent,…
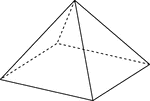
Rectangular Pyramid
Illustration of a right rectangular pyramid with hidden edges shown. The base is a rectangle and the…
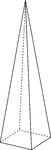
Rectangular Pyramid
Illustration of a right rectangular pyramid with hidden edges shown. The base is a rectangle and the…
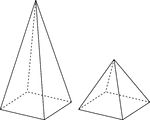
2 Right Rectangular Pyramids
Illustration of 2 right rectangular pyramids with hidden edges shown. The rectangular bases are congruent,…

Skewed Rectangular Pyramid
Illustration of a non-right, or skewed, rectangular pyramid with hidden edges shown. The base is a rectangle…
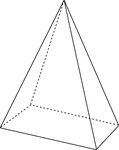
Rectangular Pyramid
Illustration of a right rectangular pyramid with hidden edges shown. The base is a rectangle and the…
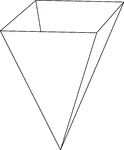
Inverted Rectangular Pyramid
Illustration of a hollow right rectangular pyramid. The base is a rectangle and the faces are isosceles…
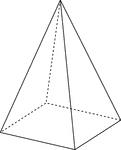
Rectangular Pyramid
Illustration of a right rectangular pyramid with hidden edges shown. The base is a rectangle and the…
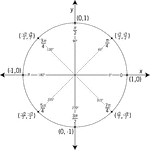
Unit Circle Labeled In 45 ° Increments
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
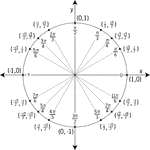
Unit Circle Labeled With Special Angles And Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
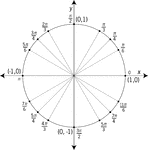
Unit Circle Labeled At Special Angles
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…

Unit Circle Labeled At Special Angles
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
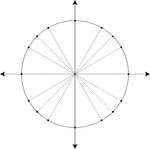
Unit Circle Marked At Special Angles
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane. All…
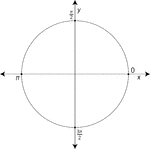
Unit Circle Labeled At Quadrantal Angles
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
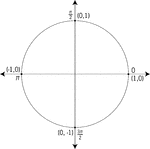
Unit Circle Labeled With Quadrantal Angles And Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane. All…
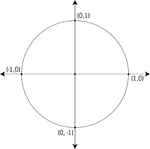
Unit Circle Labeled With Quadrantal Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane. At each…
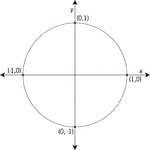
Unit Circle Labeled With Quadrantal Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
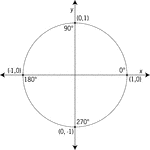
Unit Circle Labeled With Quadrantal Angles And Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…