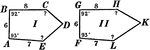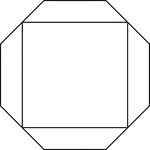
Octagon Circumscribed About a Square
Illustration of a regular octagon circumscribed about a square. This could also be described as a square…
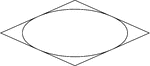
Rhombus Circumscribed About an Ellipse
Illustration of a rhombus circumscribed about an ellipse. This could also be described as an ellipse…

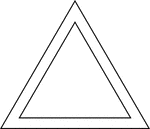
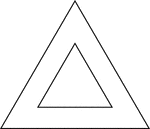
Equilateral Triangle Inscribed In An Equilateral Triangle
Illustration of an equilateral triangle inscribed in an equilateral triangle. The smaller triangle is…
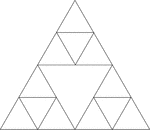
Equilateral Triangles Inscribed In An Equilateral Triangle
Illustration of an equilateral triangle inscribed in an equilateral triangle by joining the midpoints…
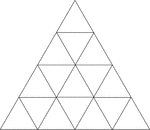
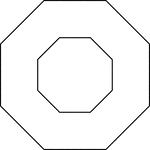
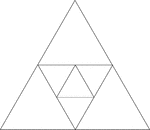
Equilateral Triangles Inscribed In Equilateral Triangles
Illustration of an equilateral triangle inscribed in an equilateral triangle by joining the midpoints…
Equilateral Triangles Inscribed In Equilateral Triangles
Illustration of an equilateral triangle inscribed in an equilateral triangle by joining the midpoints…
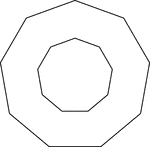
3 Concentric Equilateral Triangles
Illustration of 3 concentric equilateral triangles that are equally spaced.

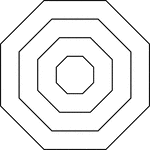
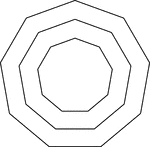
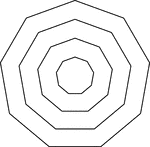
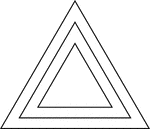
4 Concentric Equilateral Triangles
Illustration of 4 concentric equilateral triangles that are equally spaced.
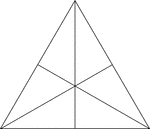
Centers of Equilateral Triangle
Illustration of an equilateral triangle that shows both the centroid (where the medians of the sides…
10 Congruent Rotated Equilateral Triangles
Illustration of 10 congruent equilateral triangles that have the same center. Each triangle has been…
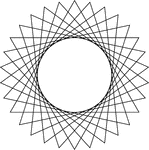
10 Congruent Rotated Equilateral Triangles
Illustration of 10 congruent equilateral triangles that have the same center. Each triangle has been…

5 Congruent Rotated Equilateral Triangles
Illustration of 5 congruent equilateral triangles that have the same center. Each triangle has been…
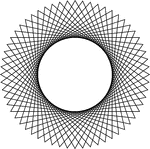
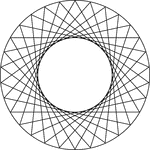
20 Congruent Rotated Equilateral Triangles
Illustration of 20 congruent equilateral triangles that have the same center. Each triangle has been…

12-Point Star Inscribed In A Dodecagon
Illustration of a 12-point star (24-sided polygon) inscribed in a regular dodecagon. This can also be…
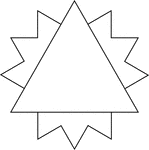
Triangle Inscribed In A 12-Point Star
Illustration of an equilateral triangle inscribed in a closed concave geometric figure with 24 sides…
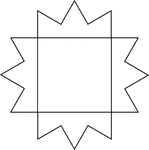
Square Inscribed in a 12-Point Star
Illustration of a square inscribed in a closed concave geometric figure with 24 sides in the shape of…
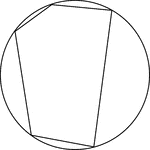
Cyclic Pentagon
Illustration of a cyclic pentagon, a pentagon inscribed in a circle. This can also be described as a…
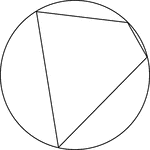
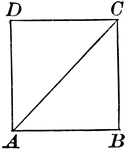
Cyclic Quadrilateral
Illustration of a cyclic quadrilateral, a quadrilateral inscribed in a circle. This can also be described…
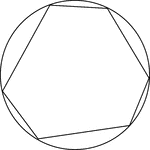
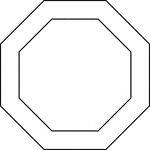
Cyclic Hexagon
Illustration of a cyclic hexagon, a hexagon inscribed in a circle. This can also be described as a circle…
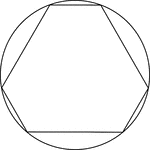
Cyclic Hexagon
Illustration of a cyclic hexagon, a hexagon inscribed in a circle. This can also be described as a circle…
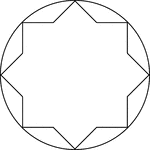
Star Inscribed In A Circle
Illustration of an 8-point star, or convex polygon, inscribed in a circle. This can also be described…
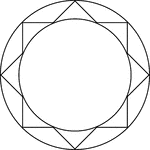
Star Inscribed And Circumscribed About Circles
Illustration of an 8-point star (convex polygon) inscribed in a large circle and circumscribed about…
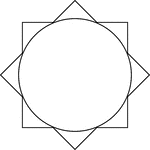
Star Circumscribed About A Circle
Illustration of an 8-point star (convex polygon) circumscribed about a circle. This can also be described…
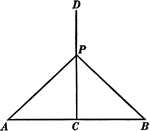
Triangle With Perpendicular Bisector
Illustration showing a perpendicular bisector of a triangle extended outside of the triangle.
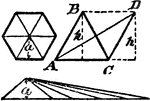
Area Of Regular Polygon Proof
An illustration showing that the area of a regular polygon is equal to the area of a triangle whose…
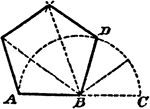
Construction Of A Regular Polygon On A Line
An illustration showing how to construct a regular polygon on a given line without resort to its center.…

Circle Sector
An illustration showing a circle sector with center/central angle v and polygon angle w.
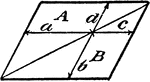
Model Of Geometric Proportions
An illustration showing a quadrilateral model that illustrates the following relationships: a:b = c:d,…
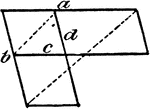
Model Of Geometric Proportions
An illustration showing a model that illustrates the following relationships: a:b = c:d, ad = bc. Product…
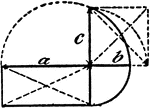
Model Of Geometric Proportions
An illustration showing a model that illustrates the following relationships: a:b = c:b, ab = c²,…
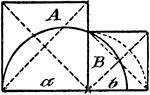
Model Of Geometric Proportions
An illustration showing a model that illustrates the following relationship: A:B = a:b.
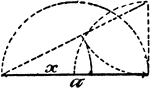
Model Of Geometric Proportions
An illustration showing a model that illustrates the following relationships: a:x = x:a - x, x = √(a²…
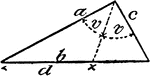
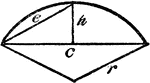
Model Of Geometric Proportions In A Triangle
An illustration showing a model of a triangle that illustrates the following relationship: a:c = d:(b…

Pyramids
An illustration of two pyramids. A pyramid is a building where the upper surfaces are triangular and…

Polygonal Masonry
Polygonal masonry is a technique of stone construction of the ancient Mediterranean world. True polygonal…
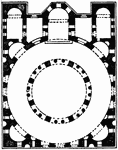
Cathedral at Bosra
Circular and polygonal plans appear in a number of Syrian examples of the early sixth century. Their…
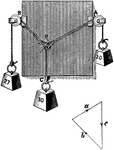
Polygon of Forces
"In the apparatus shown... three forces act on a small body and are allowed to assume a position of…
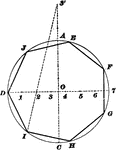
Construction Of Polygon Inscribed In Circle
Illustration used to show how to inscribe any regular polygon in a given circle.
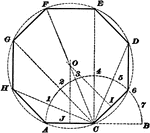
Construction Of Regular Polygon
Illustration used to show how to draw a regular polygon when given a side of the polygon.
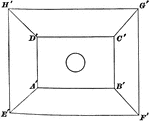
Circle Inside Concentric Rectangles
Illustration of a circle inside of 2 concentric rectangles whose vertices are connected by line segments.
Double Arch
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
Arch
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…

Triangular Double Arch
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…

Bear
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…