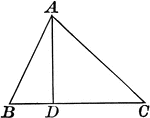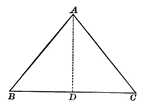
Isosceles Triangle With Interior Segment Drawn
Illustration showing an isosceles triangle with a segment inside. This can be used to show that in an…
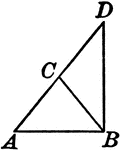
Leg Produced through the Vertex of an Isosceles Triangle
Illustration to show that if one of the legs of an isosceles triangle is produced through the vertex…

Medians Drawn Drawn to Legs of Isosceles Triangles
Illustration to show the medians drawn to the legs of an isosceles triangle.
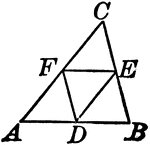
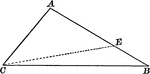
Midpoints of Triangle Divide Triangle into Four Equal Triangles
Illustration to show that if the lines joining the middle points of the sides of a triangle divide the…
Orthocenter of Triangle
Illustration to show altitudes in a triangle. It is known as the orthocenter.
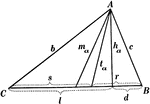
Parts Of A Triangle
Illustration used to show the various parts of a triangle: sides, angles, medians, altitudes, bisectors,…
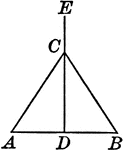
Perpendicular Bisector of the Base of an Isosceles Triangle
Illustration to show that the perpendicular bisector of the base of an isosceles triangle passes through…
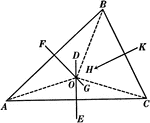
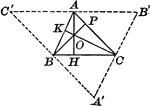
Perpendicular Bisectors In A Triangle
Illustration used to prove "The perpendicular bisectors of the sides of a triangle are concurrent in…
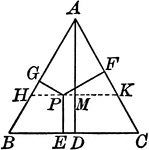
Perpendiculars Dropped Any Point in the Equilateral Triangle
Illustration to show the perpendiculars dropped from any point in the equilateral triangle to the three…
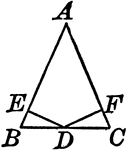
Perpendiculars Dropped From Midpoint of Base to Legs of Isosceles Triangles
Illustration to show the perpendiculars dropped from the midpoint of the base to the legs of an isosceles…
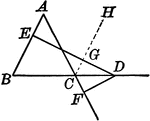
Point in Base of Isosceles Triangle
Illustration to show that the difference of the distances from any point in the base produced of an…
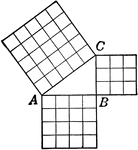
Pythagorean Theorem Triangle
Right triangle with squares that can be used to illustrate the Pythagorean Theorem.
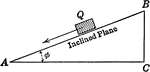
Inclined Plane Forming Right Triangle
Inclined plane forming right triangle showing the velocity of a body sliding a distance,s, down a smooth…
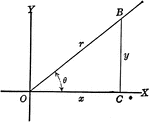
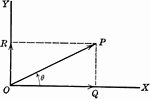
Right Triangle OCB With, x, y, and r shown
Right triangle OCB that can be used to show the relationships between x, y, r, and Θ.
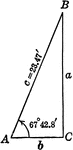
Right Triangle ABC With Angle 67 degrees 42.8 minutes and Hypotenuse 23.47 ft.
Right triangle ABC with a base angle of 67 degrees 4208 minutes and a hypotenuse of 23.47 ft.

Right Triangle ABC With Leg 23.85 ft. and Hypotenuse 35.62 ft.
Right triangle ABC with a leg of 23.85 feet and a hypotenuse of 35.62 feet.
Right Triangle With One Angle Double the Other
Illustration of a right triangle with one angle the double of the other.
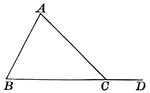
Triangle With Segment Extended for Exterior Angle
Illustration showing a triangle with an exterior segment drawn to show and exterior angle. This can…
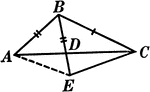
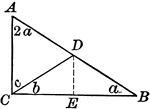
Segments Labeled In A Triangle
Illustration of triangle ABC with BE extended through the triangle at point D. Segment AB is equal to…
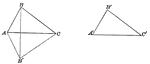
Equal Triangles by Side Side Side
Illustration showing two equal triangles. This can be used to show that two triangles are equal if the…
Proof of Equal Triangles Drawing
Illustration to show if two triangles have two sides of the one equal, respectively, to two sides of…
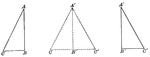
Equal Right Triangles by Hypotenuse Leg
Illustration showing two equal right triangles. This can be used to show that two right triangles are…
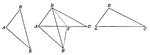
Three Triangles Used to Compare Sides
Illustration showing three triangles. This is used to show the following theorem: If two triangles have…
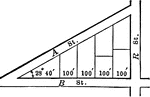
Triangular City Block With Angles and Lengths
Illustration showing an angle of 23 degrees 40 minutes making a triangle in a city block and marking…
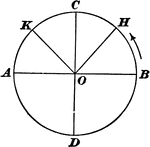
Arcs and Angles of a Trigonometric Circle
"In trigonometry, the arcs of circles are used to measure angles. All angles are supposed to have their…
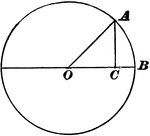
Trigonometry Triangle to Show Sine, Cosine, and Tangent
Right triangle OCA, inside of Circle O is used to show that side AC is "opposite" O and side OC is "adjacent"…
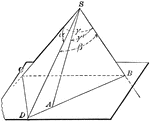
Face Angles of Trihedral Angle
Diagram used to prove the theorem: "The sum of two face angles of a trihedral angle is greater than…
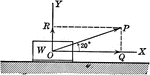
Vector Showing Force at Angle of 20 degrees
OP is a vector (directed quantity) showing the force by a weight acting on it at an angle of 20 degrees.