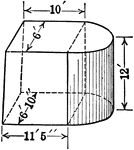
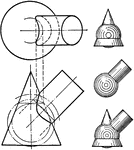
Composite Figure of Quadrilateral Frustum With Half of a Cylinder Attached
An illustration of a composite figure made up of a quadrilateral frustum and half of a cylinder. Frustum…

Cross Section of Concrete Conduit
Cross section of concrete conduit. The diagram can be used to find volume.

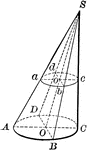
Cone
"A cone is a solid whose base is a circle and whose convex surface tapers uniformly to a point." —Hallock…
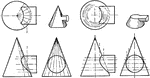
Development Exercise of Cone
Development and top completion exercise problem of the cone by dividing the base into equal parts and…
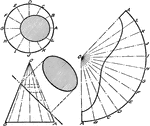
Development of Cone
A rolled out image of a cone by dividing the base in equal parts and arcs to measure the true lengths.
Plane Parallel to Base, Passing Through a Cone
Illustration of a plane parallel to the base passing through a cone (section made is a circle).
Plane Parallel to Base, Passing Through a Cone
Illustration of a plane parallel to the base passing through a cone (section made is a circle).
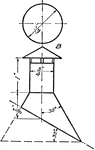
Development Exercise of Flange and Hood Cones
An exercise problem to complete the top and develop, stretched out, image of the flange and hood cones…
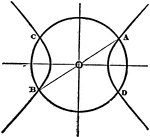
Conic Axes
Conjugate diameters perpendicular to each other are called, axes, and the points where they cut the…

Conic Section Using Circle
The cone is sliced by a circle in a plane perpendicular to the axis. This can be drawn without knowledge…

Conic Section Using Ellipse
The cone is sliced by a ellipse by making an angle within the plane. This can be drawn with knowing…
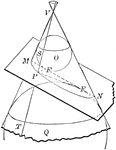
Cone depicting Conic Sections
Diagram of a cone with spheres and cut by a plane to depict the conic sections.
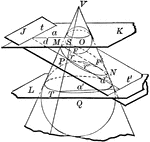
Cone depicting Conic Sections
Diagram of a cone with inscribed spheres and cut by various planes to depict the conic sections: circle,…
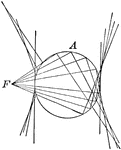
Construction of a Conic
Diagram showing how to construct a conic when given the focus and the auxiliary circle. If the focus…

Focus In Auxiliary Circle of Conic
Diagram showing how to construct a conic when given the focus and the auxiliary circle. The focus is…
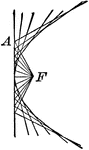
Focus In Auxiliary Circle of Conic
Diagram showing how to construct a conic when given the focus and the auxiliary circle. As the focus…
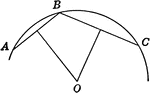
Construction of Arc When Given the Chord and Height of the Segment
Illustration of of construction of an arc when the chord and height of the segment are given.
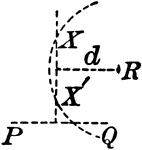
Construction of a Circle When Given Two Points and a Radius
Illustration used to construct a circle when given two points that it passes through and a radius.

Triangle With Circle Constructions
Illustration of a triangle with its incircle and three excircles constructed.
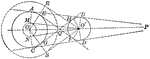
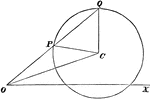
Construction of a Common Tangent When Given Two Circles
Illustration used to construct a common tangent when given two circles.
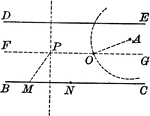
Construction of a Circle Through a Given Point that Cuts Chords of Given Lengths From Parallels
Illustration used to construct a circle that shall pass through a given point and cut chords of a given…
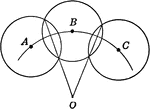
Construction of Radius When Given Only a Part of the Circumference
Illustration of of construction of a radius when given only a part of the circumference.
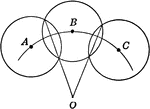
Construction of Radius When Given Only a Part of the Circumference
Illustration of of construction of a radius when given only a part of the circumference.
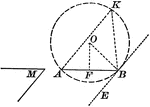
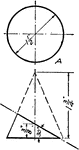
Construction to Describe a Segment of a Circle in Which an Angle Can Be Inscribed
Illustration of the construction used upon a given straight line, to describe a segment of a circle…
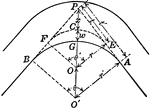
Curve in Pavement of Road
Illustration of blueprint used by highway engineers to widen the pavement on the inside of the curve…
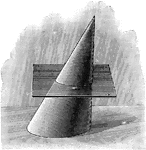
Intersection of Cylinder and Cone
An illustration of finding an intersection of a cone and cylinder by either cutting the vertex of the…
Cycloid
"A cycloid is the curve generated by the motion of a point on the circumference of a circle rolled along…
Intersection of Cylinder and Cone
An illustration of finding an intersection of a cone and cylinder by either cutting the vertex of the…
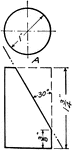
Development Exercise of Cylinder
An exercise problem in creating a development or rolled out surface of a cylinder in a 4" by 5" drawing…
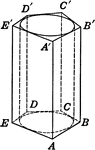
Cylinder Inscribed in Pentagonal Prism
Right circular cylinder inscribed in a pentagonal prism. Or, Pentagonal prism circumscribed about a…
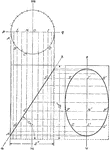
Plane Intersecting A Cylinder
Illustration of a cylinder cut by a plane making an angle of 57° with the base.
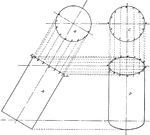
Projection of Cylinder
Illustration of the method of finding the projection, in the form of an ellipse, of the top of a cylinder…

Right Cylinder
a solid which may be concieved as generated by the revolution of a rectangle about one of its sides.
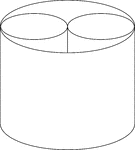
2 Smaller Cylinders In A Larger Cylinder
A large cylinder containing 2 smaller congruent cylinders. The small cylinders are externally tangent…
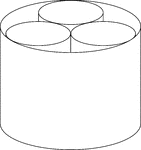
3 Smaller Cylinders In A Larger Cylinder
A large cylinder containing 3 smaller congruent cylinders. The small cylinders are externally tangent…
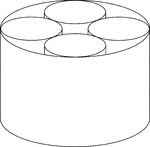
4 Smaller Cylinders In A Larger Cylinder
A large cylinder containing 4 smaller congruent cylinders. The small cylinders are externally tangent…
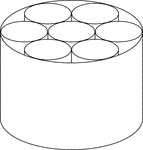
7 Smaller Cylinders In A Larger Cylinder
A large cylinder containing 7 smaller congruent cylinders. The small cylinders are externally tangent…
Construction Of A Cyma
An illustration showing how to construct a cyma, or two circle arcs that will tangent themselves, and…

Design Similar to Yin Yang Symbol
Design made by drawing one large circle and then two circles that are vertically placed and internally…

Circular Design
Circular design made by rotating circles about a fixed point. The radii of the smaller circles is equal…

Circular Design
Circular design made by rotating circles about a fixed point. The radii of the smaller circles is equal…
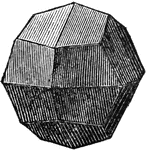
Diploid
A solid belonging to the isometric system, with 24 trapezoidal planes. It is the parallel hemihedral…
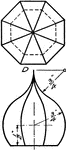
Development Exercise of Dome and True Shape of Hip
A development or rolled out image exercise problem of the dome and finding the true shape of the hip,…

Drawing a Circle Using Compass
When drawing the circle, the compass is turned by the handle with the thumb and forefinger in a clockwise…
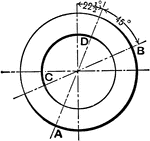
Drawing Lines 4
Circles should be unshaded or shaded evenly with thick and thin lines, changing at about 45 degrees.
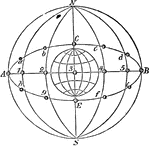
Suns in the Equator and Ecliptic
"Were the Earth's orbit a perfect circle, and her axis perpendicular to the plane of this orbit, the…
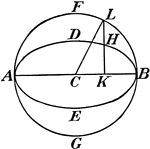
Eccentric Angle
"In geometry, an angle connected with an ellipse and defined as ... angle BCL, reckoned from one determinate…

Construction of Ellipse by Describing Circles
Illustration used to draw a an ellipse using string and pins by describing a circles with diameters…
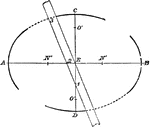
Construction of Ellipse
Illustration used to draw a an ellipse with major axis AB and minor axis CD.
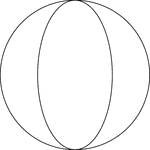
Ellipse Inscribed In A Circle
Illustration of an ellipse, whose major axis is vertical, inscribed in a circle whose diameter is equal…
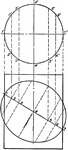
Section of a Cylinder Showing an Ellipse
Illustration showing an ellipse (and circle) as a section from a cylinder.
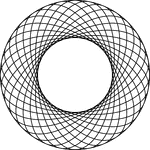
16 Rotated Concentric Ellipses
Illustration of 16 concentric congruent ellipses that are rotated about the center at equal intervals…