Diagram Illustrating Astigmatism
An illustration depicting an astigmatism. An optical system with astigmatism is one where rays that…
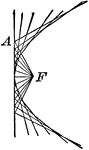
Construction of a Conic
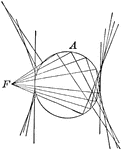
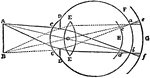
Diagram showing how to construct a conic when given the focus and the auxiliary circle. If the focus…
Focus In Auxiliary Circle of Conic
Diagram showing how to construct a conic when given the focus and the auxiliary circle. The focus is…
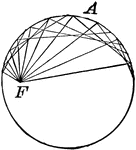
Focus In Auxiliary Circle of Conic
Diagram showing how to construct a conic when given the focus and the auxiliary circle. As the focus…
Corresponding Points in an Ellipse and Circle
Illustration of half of an ellipse. "The ordinates of two corresponding points in an ellipse and its…
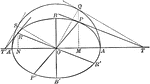
Conjugate Diameters of an Ellipse
Illustration showing that if one diameter is conjugate to a second, the second is conjugate to the first.
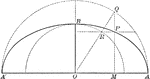
Construction of an Ellipse
Illustration of half of an ellipse and its auxiliary circle used to construct an ellipse by points,…
Construction of an Ellipse
Diagram showing how to construct an ellipse when given the two foci and the length of the major axis…
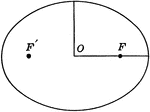
Definition of Ellipse
Diagram of an ellipse that can used to illustrate the definition. "The constant ration between the distances…
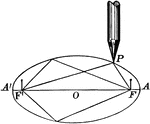
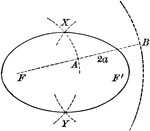
Demonstration of Ellipse Definition
Illustration showing the definition of an ellipse. "An ellipse is a curve which is the locus of a point…
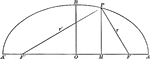
Focal Radii of an Ellipse
Illustration of half of an ellipse. "If d denotes the abscissa of a point of an ellipse, r and r' its…
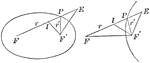
Foci Distances on an Ellipse
Diagram that illustrates "The algebraic sum of the distances of any point from the foci of a conic is…
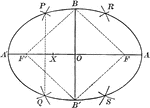
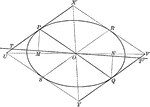
Ellipse With Parts Labeled
Illustration of an ellipse with foci F' and F, major axis A' to A, minor axis B' to B, and center O.
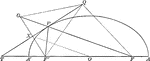
Line Bisecting Angle Between Focal Radii on Ellipse
Illustration of half of an ellipse. "If through a point P of an ellipse a line is drawn bisecting the…
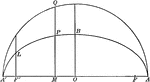
Ordinate and Major Axis of Ellipse
Illustration of half of an ellipse. The square of the ordinate of a point in an ellipse is to the product…
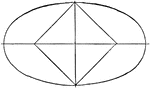
Parallel Tangents to an Ellipse
Illustration showing that tangents drawn at the ends of any diameter are parallel to each other.
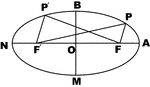
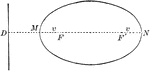
Parts of Ellipse
Diagram of an ellipse that can used to illustrate the different parts. Segment MN is the major axis,…
Point Distances to Foci on Ellipse
Illustration of half of an ellipse. "The sum of the distances of any point from the foci of an ellipse…
Tangent From External Point to an Ellipse
Illustration of how to draw a tangent to an ellipse from an external point.
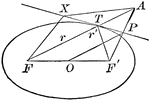
Tangent to an Ellipse
Diagram an ellipse with a tangent line that illustrates "A line through a point on the ellipse and bisecting…
Tangents to an Ellipse
Illustration showing the tangents drawn at two corresponding points of an ellipse and its auxiliary…
Lens of the eye
"Diagram showing the Change in the Lens during Accomadation. On the right the lens is arranged for distant…
Focus
"A fire-place; a hearth; a brazier. The fire-place possessed a sacred character, and was dedicated among…
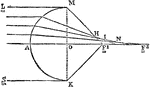
Formation of Circles of Diffusion
An illustration depicting the formation of circles of diffusion. "From point A luminous rays enter the…

Reflection of Radiant Heat
"Heat is radiated at C, which is placed at mirror A's focus. Mirror A catches some of the heat and reflects…
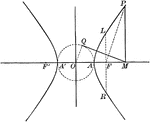
Auxiliary Circle and Hyperbola
Illustration of a hyperbola and its auxiliary circle. "Any ordinate of a hyperbola is to the tangent…
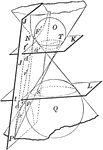
Cone Intersected by a Plane to Form a Hyperbola
Diagram depicting a cone with both nappes intersected by plane J to form a hyperbola.
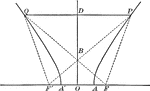
Conjugate Axis of a Hyperbola
Illustration showing how the a hyperbola is symmetrical with respect to its conjugate axis.
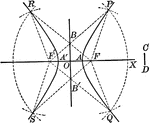
Construction of Hyperbola
Illustration showing how a hyperbola con be constructed by points, having been given the foci and the…
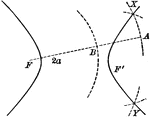
Construction of a Hyperbola
Diagram showing how to construct a hyperbola when given the two foci and the length of the major axis…
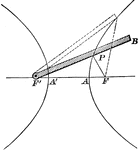
Demonstration of Hyperbola Definition
Illustration showing the definition of an hyperbola. "An hyperbola may be described by the continuous…
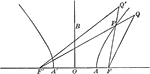
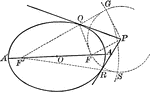
Foci Distance of Hyperbola
Illustration of a hyperbola with distances to foci drawn. "The difference of the distances of any point…
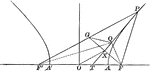
Line Bisecting Angle Between Focal Radii in Hyperbola
Illustration of a hyperbola with a line bisecting the focal radii. "If through a point P of an hyperbola…
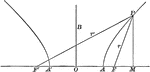
Point on a Hyperbola
Illustration of a point on a hyperbola. "If d denotes the abscissa (x-coordinate) of a point of an hyperbola,…
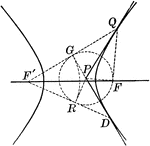
Tangent to Hyperbola
Illustration showing how to draw a tangent to an hyperbola from a given point P on the convex side of…
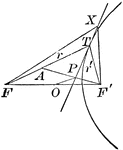
Tangent to a Hyperbola
Diagram part of a hyperbola with a tangent line that illustrates "A line through a point on the hyperbola…
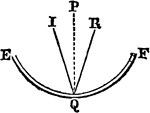
Concave Mirror
"A concave mirror reflects from a curved surface hollowing in like he inside of an orange." —Quackenbos…
Focus of a Concave Mirror
"The focus of a concave mirror is the point where the rays are brought together by reflection." -Comstock…
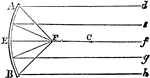
Reflection from Concave Mirrors
"Parallel rays of light strike the concave mirror. The rays converge at the focus, F, which is halfway…
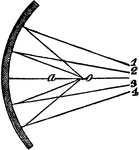
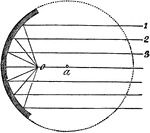
Divergent Rays in a Concave Mirror
"...be made obvious...where the diverging rays 1, 2, 3, 4 form a focus at the point o, whereas, had…
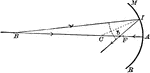
Rays Diverging from Beyond the Center of Curvature on a Concave Mirror
"When the rays diverge from a point beyond the center of curvature, as B, the focus falls on the same…
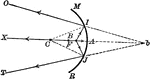
Rays Diverging from Beyond the Center of Curvature on a Concave Mirror
"When the rays diverge form a point at a distance from the mirror less than that of the principal focus,…
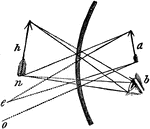
Concave Mirror with Image and Focus
"The focus of each point chose may be determined by tracing two rays from the point, and locating their…
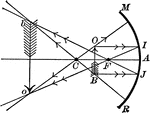
Image Beyond the Curvature of a Concave Mirror
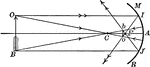
"When the object is at a distance from the mirror somewhat greater than the center of curvature, as…

Object Beyond the Focus in a Concave Mirror
"...if the object is placed more remote from the mirror than the principal focus, and between the focus…
Object Within the Focus in a Concave Mirror
"...let us suppose the object a, to be placed before the mirror, and nearer to it than the principal…
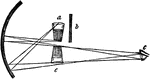
Deception by Mirrors
"Suppose the tumbler, a, to be filled with water, and placed beyond the principal focus of the concave…
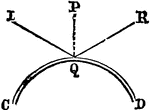
Convex Mirror
"A convex mirror reflects from a curved surface rounding out like the outside of an orange." —Quackenbos…
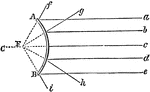
Reflection by Convex Mirrors
"Parallel rays strike the convex mirror, reflect, and diverge as if they had originated from a virtual…
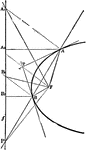
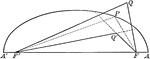
Parabola Foci Properties
The segments between the point of intersection of two tangents to a conic and their points of contact…
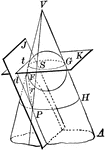
Cone Intersected by a Plane to Form a Parabola
Diagram of a cone intersected by plane J to form a parabola. Also pictured is a circle formed by the…

Conic Section Showing Parabola
Illustration showing the definition of a parabola as a conic section. "The section of a right circular…
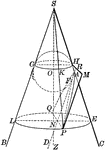
Conic Section Showing Parabola
Illustration showing the definition of a parabola as a conic section. "The section of a right circular…
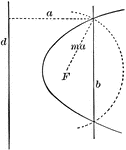
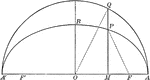
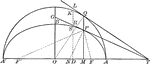
Construction of a Parabola
Diagram showing how to construct a parabola when given the directrix (d), the focus (F) and the eccentricity…
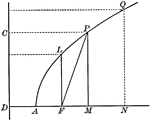
Parabola With Coordinates and Latus Rectum
Illustration of a parabola showing that any point of a parabola is the mean proportional between the…
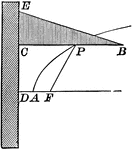
Parabola With Focus and Directrix
Illustration of a parabola - a curve which is the locus of a point that moves in a plane so that its…