Clipart tagged: ‘respiration’
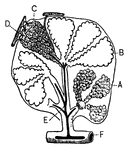
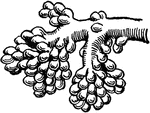
Capillaries of the Air Sac
"Diagram showing the capillary network of the air sacs and origin of the pulmonary veins.. A,…
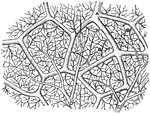
Diagrammatic view of an air sac
"A, epithelial lining wall; B, partition between two adjacent sacs, in which run capillaries;…

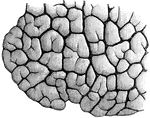
Two Alveoli of the Lung
Two alveoli of the lung, highly magnified. Alveoli are cavities which are honeycombed with bulgings…
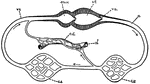
Blood Circulation
This illustration shows a representation of the circulation of the blood, in its essential features.…
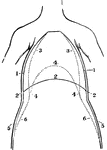
A Front View of the Chest and Abdomen in Respiration
A front view of the chest and abdomen in respiration. Labels: 1, The position of the walls of the chest…

A Side View of the Chest and Abdomen in Respiration
A side view of the chest and abdomen in respiration. Labels: 1, The cavity of the chest. 2, The cavity…
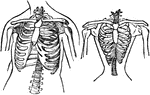
Natural and Contracted Chest
The left figure represents the natural shape of the chest, and that upon the right, the contracted state…
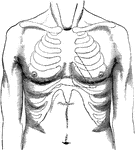
Surface of Normal Chest
Surface of normal chest; outlines of cardiac dulness to the left of the sternum. The spaces enclosed…

Structure of the Chest
Structure of the chest, showing the framework of the bones which are connected together chiefly by muscles.…
![Torso of the Statue known as Venus of Melos (left) and New York Fashion, 1898 (right). "Since abdomen and chest alternately expand and contract in healthy breathing, anything which impedes their free movement is to be avoided. The tight lacing which is still indulged [in 1900] by those who think a distorted form beautiful, seriously impedes one of the most important functions of the body, and leads not only to shortness of breath and an incapacity for muscular exertion, but in many cases to actual deformity or disease." — Newell, 1900.](https://etc.usf.edu/clipart/36200/36290/corset_36290_mth.gif)
Effect of Corset Use on Respiration
Torso of the Statue known as Venus of Melos (left) and New York Fashion, 1898 (right). "Since abdomen…
![Torso of the Statue known as Venus of Melos (left) and New York Fashion, 1898 (right). "Since abdomen and chest alternately expand and contract in healthy breathing, anything which impedes their free movement is to be avoided. The tight lacing which is still indulged [in 1900] by those who think a distorted form beautiful, seriously impedes one of the most important functions of the body, and leads not only to shortness of breath and an incapacity for muscular exertion, but in many cases to actual deformity or disease." — Newell, 1900.](https://etc.usf.edu/clipart/36200/36291/corset_36291_mth.gif)
Effect of Corset Use on Respiration
Torso of the Statue known as Venus of Melos (left) and New York Fashion, 1898 (right). "Since abdomen…

Cray-fish
"Diagrammatic cross-section of Cray-fish in the thoracic region, to show relation of circulation and…

Respiration Diagram
A diagram of how respiration works. A balloon is attached to the end of a small oil lamp chimney. The…
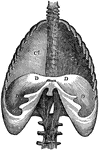
The Diaphragm
The diaphragm, which is the principal muscle that act sin breathing. Here you have the cavity of the…
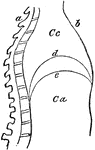
The Diaphragm
Diaphragm of the diaphragm and it's placement in the chest. Let a represent the spinal column,…

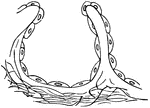
Gills (Branchial Arch of Perch)
This illustration shows the gills (breathing apparatus) of a perch, as well as the specific veins and…

Gills (Crayfish)
This illustration shows the thorax of a crayfish with a portion of the carapace removed to show the…

Gills (worm)
This illustration shows a transverse section of a worm with external gills. Gills are the breathing…
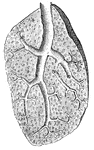
Lobule of a Lung
"Showing the structure of a lobule of the lung. The lobule has been injected with mercury, afterwards…

Lungs
"Relative Postion of the Lungs, the Heart, and Some of the Great Vessels belonging to the latter. A,…
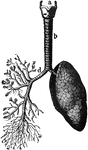
Lungs and Air Passages
The lungs and air passages seen from the front. On the left of the figure the pulmonary tissue has been…
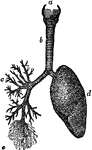
Structure of the Lungs
Diagram showing the structure of the lungs. At d is the left lung, and at c are represented…
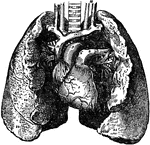
The Lungs
The lung, which are the two essential organs of respiration contained in the cavity of the thorax.
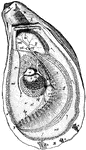
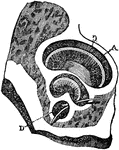
Oyster
"Anatomy of the Oyster. A. Hinge or anterior umbonal end of the left valve of an adult oyster, upon…
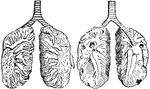
Lungs of a Pigeon
"The external air penetrates into every part of their body by the respiratory tubes, which ramify the…
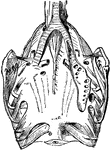
Respiratory Organs of a Pigeon
"The external air penetrates into every part of their body by the respiratory tubes, which ramify the…
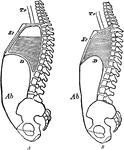
Changes during Respiration
Diagram to show the changes in the sternum, diaphragm, and abdominal wall in respiration. Labels: A,…
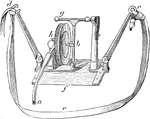
Stethograph or Pneumograph
The stethograph or pneumograph consists of a thick rubber of elliptical shape about three inches long,…
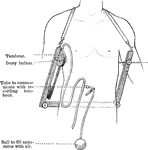
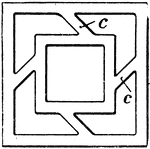
Stethometer
The stethometer consists of a frame formed of two parallel steel bars joined by a third at one end.…
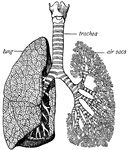
Trachea and lungs
"The trachea has in its walls stiff rings of cartilage that hold it open so that the air can…

Worker with Mouthpiece
"A workman wearing a mouthpiece to protect himself from dust." — Ritchie, 1918