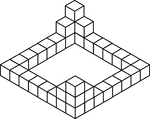
36 Stacked Congruent Cubes
Illustration of 36 congruent cubes stacked at various heights with outer edges forming a square. A 3-dimensional…

36 Stacked Congruent Cubes
Illustration of 36 congruent cubes stacked to resemble a 1 by 1 by 1 cube on a 2 by 2 by 2 cube on a…

39 Stacked Congruent Cubes
Illustration of 39 congruent cubes stacked at various heights. A 3-dimensional representation on a 2-dimensional…

4 Stacked Congruent Cubes
Illustration of 4 congruent cubes stacked in ones and twos. A 3-dimensional representation on a 2-dimensional…
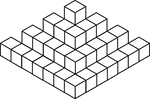
50 Stacked Congruent Cubes
Illustration of 50 congruent cubes stacked at various heights. A 3-dimensional representation on a 2-dimensional…
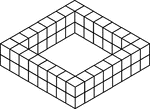
56 Stacked Congruent Cubes
Illustration of 56 congruent cubes stacked in twos in the shape of a square. A 3-dimensional representation…

56 Stacked Congruent Cubes
Illustration of 56 congruent cubes stacked in heights of 1, 4, and 5 cubes that form a zigzag pattern.…
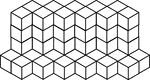
57 Stacked Congruent Cubes
Illustration of 57 congruent cubes stacked in heights of 1 and 5 cubes that form a zigzag pattern. A…
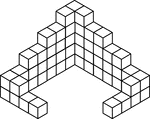
59 Stacked Congruent Cubes
Illustration of 59 congruent cubes stacked at various heights. A 3-dimensional representation on a 2-dimensional…
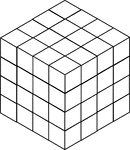
64 Stacked Congruent Cubes
Illustration of 64 congruent cubes stacked so they form a cube that measures 4 by 4 by 4. A 3-dimensional…
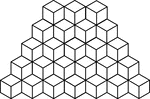
65 Stacked Congruent Cubes
Illustration of 65 congruent cubes stacked at heights increasing from 1 to 5 cubes. A 3-dimensional…
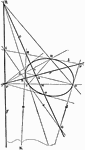
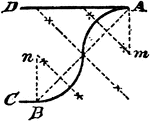
Second Order Curve Tangents
Any four-point on a curve of the second order and the four-side formed by the tangents at these points…
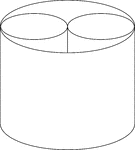
2 Smaller Cylinders In A Larger Cylinder
A large cylinder containing 2 smaller congruent cylinders. The small cylinders are externally tangent…

3 Congruent Tangent Right Circular Cylinders
Illustration of 3 right congruent tangent circular cylinders. The height of all the cylinders is greater…
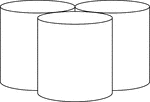
3 Congruent Tangent Right Circular Cylinders
Illustration of 3 right congruent tangent circular cylinders.
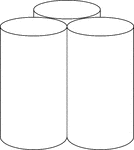
3 Congruent Tangent Right Circular Cylinders
Illustration of 3 right congruent tangent circular cylinders. The height of all the cylinders is greater…
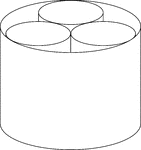
3 Smaller Cylinders In A Larger Cylinder
A large cylinder containing 3 smaller congruent cylinders. The small cylinders are externally tangent…
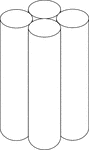
4 Congruent Tangent Right Circular Cylinders
Illustration of 4 congruent tangent right circular cylinders. The height of all the cylinders is greater…
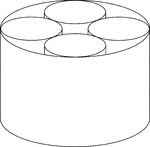
4 Smaller Cylinders In A Larger Cylinder
A large cylinder containing 4 smaller congruent cylinders. The small cylinders are externally tangent…
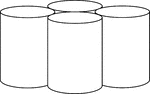
4 Tangent Cylinders
Illustration of 4 congruent cylinders with diameters less than the height. The cylinders are externally…
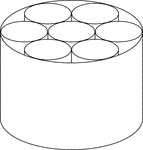
7 Smaller Cylinders In A Larger Cylinder
A large cylinder containing 7 smaller congruent cylinders. The small cylinders are externally tangent…

7 Tangent Cylinders
Illustration of 7 congruent cylinders with diameters less than the height. 6 of the cylinders are equally…

7 Tangent Cylinders
Illustration of 7 congruent cylinders with diameters less than the height. 6 of the cylinders are equally…
Construction Of A Cyma
An illustration showing how to construct a cyma, or two circle arcs that will tangent themselves, and…

12-Point Star Inscribed In A Dodecagon
Illustration of a 12-point star (24-sided polygon) inscribed in a regular dodecagon. This can also be…
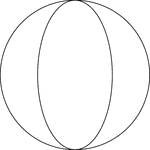
Ellipse Inscribed In A Circle
Illustration of an ellipse, whose major axis is vertical, inscribed in a circle whose diameter is equal…
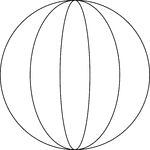
2 Ellipses Inscribed In A Circle
Illustration of 2 concentric ellipses, whose major axes are vertical, inscribed in a circle whose diameter…
2 Ellipses With Equal Vertical Axes
An illustration of 2 ellipses that have the equal vertical axes, but different horizontal axes. The…

2 Ellipses With Equal Vertical Axes
An illustration of 2 ellipses that have the equal vertical axes, but different horizontal axes. The…

3 Concentric Ellipses
An illustration of 3 concentric ellipses that are tangent at the end points of the vertical axes. The…
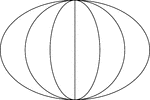
3 Concentric Ellipses
An illustration of 3 concentric ellipses that are tangent at the end points of the vertical axes, which…
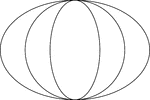
3 Concentric Ellipses
An illustration of 3 concentric ellipses that are tangent at the end points of the vertical axes. The…
4 Concentric Ellipses
An illustration of 4 concentric ellipses that are tangent at the end points of the vertical axes. The…
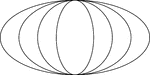
4 Concentric Ellipses
An illustration of 4 concentric ellipses that are tangent at the end points of the vertical axes. The…

4 Concentric Ellipses
An illustration of 4 concentric ellipses that are tangent at the end points of the vertical axes, which…

5 Concentric Ellipses
An illustration of 5 concentric ellipses that are tangent at the end points of the vertical axes. The…
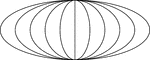
5 Concentric Ellipses
An illustration of 5 concentric ellipses that are tangent at the end points of the vertical axes, which…

6 Concentric Ellipses
An illustration of 6 concentric ellipses that are tangent at the end points of the vertical axes. The…

6 Concentric Ellipses
An illustration of 6 concentric ellipses that are tangent at the end points of the vertical axes, which…
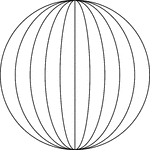
Ellipses Inscribed In A Circle
Illustration of concentric ellipses, whose major axes are vertical, inscribed in a circle whose diameter…
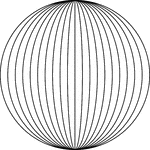
Ellipses Inscribed In A Circle
Illustration of concentric ellipses, whose major axes are vertical, inscribed in a circle whose diameter…

Construction Of An Equilateral Triangle Inscribed In A Circle
An illustration showing how to construct an equilateral triangle inscribed in a circle. "With the radius…

Centrifugal Force
"If a body be fastened to a string and whirled, so as to give it a circular motion, there will be a…

Tangent galvanometer
"The galvanometer is an instrument for determining the strength of an electric current by means of the…
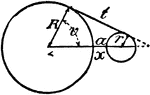
Model Of Geometric Relationships In 2 Circles
An illustration showing a model of 2 circles with tangent lines, diameters, and radii that illustrates…
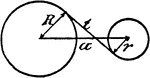
Model Of Geometric Relationships In 2 Circles
An illustration showing a model of 2 circles with tangent lines, diameters, and radii that illustrates…
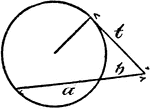
Model Of Geometric Relationships In A Circle
An illustration showing a model of a circle with an exterior angle formed between a tangent and a secant…
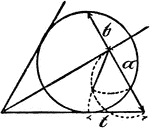
Model Of Geometric Relationships In A Circle
An illustration showing a model of a circle with angles formed between tangents and secants that illustrates…
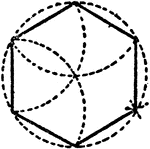
Construction Of A Hexagon In A Circle
An illustration showing how to construct a hexagon in a given circle. "The radius of the circle is equal…
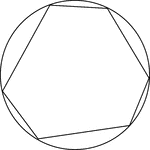
Cyclic Hexagon
Illustration of a cyclic hexagon, a hexagon inscribed in a circle. This can also be described as a circle…
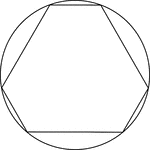
Cyclic Hexagon
Illustration of a cyclic hexagon, a hexagon inscribed in a circle. This can also be described as a circle…
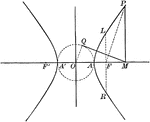
Auxiliary Circle and Hyperbola
Illustration of a hyperbola and its auxiliary circle. "Any ordinate of a hyperbola is to the tangent…
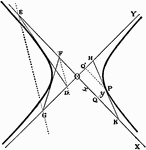
Hyperbola Tangent Triangles
All triangles formed by a tangent and the asymptotes of an hyperbola are equal in area.
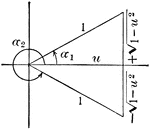
Angle Expressed As An Inverse Function
Illustration that can be used to show that when given an angle, expressed as an inverse function of…
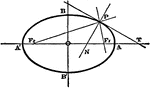
Conic Foci Involution
The lines joining any point on a conic to the two foci are equally inclined to the tangent and normal…
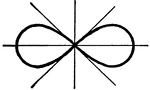
Lemniscate
A Lemniscate is, in general, a curve generated by a point moving so that the product of its distances…
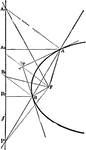
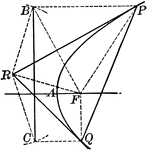
Parabola Foci Properties
The segments between the point of intersection of two tangents to a conic and their points of contact…

Tangents and Chords of a Parabola
Illustration showing that the area of a parabolic segment made by a chord is two thirds the area of…