Construction Of A Pentagon Inscribed In A Circle
An illustration showing how to construct a pentagon inscribed in a circle. "Draw the diameter AB, and…
Construction Of A Pentagon On A Line
An illustration showing how to construct a pentagon on a given line. "From B erect BC perpendicular…
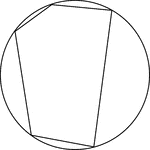
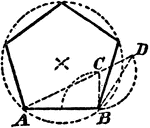
Cyclic Pentagon
Illustration of a cyclic pentagon, a pentagon inscribed in a circle. This can also be described as a…
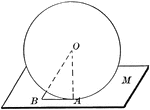
Sphere Tangent to Plane
Diagram used to prove the theorem: "A plane perpendicular to a radius at its extremity is tangent to…
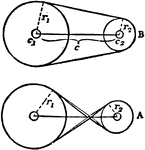
Pulley
Two arrangements of pulley: crossed belt and uncrossed belt. The pulleys are constructed with two circles…

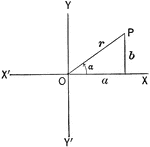
Triangles and Sectors in Quadrant I
Illustration of an angle &alpha with the vertex at the center, O, of a circle with radius OB. AC and…
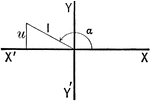
Triangle in Quadrant I
Illustration of an angle &alpha with the terminal side used to draw a triangle in quadrant I.
Triangle in Quadrant II
Illustration of an angle with the terminal side used to draw a triangle in quadrant II.
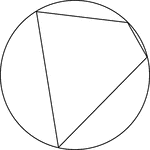
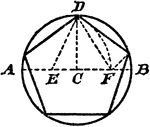
Cyclic Quadrilateral
Illustration of a cyclic quadrilateral, a quadrilateral inscribed in a circle. This can also be described…
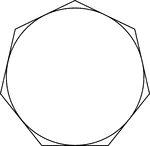
Regular Heptagon/Septagon Circumscribed about a Circle
Illustration of a regular heptagon/septagon circumscribed about a circle. This can also be described…

Circle with Secant
A secant is "a line which cuts a figure in any way. Specifically, in trigonometry, a line from the center…

Construction Of A Square Circumscribed About A Circle
An illustration showing how to construct a square circumscribed about a circle. "Draw the diameters…
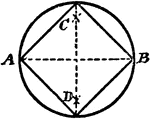
Construction Of A Square Inscribed In A Circle
An illustration showing how to construct a square inscribed in a circle. "Draw the diameter AB, and…
Skyscraper Giant Stepladder
Illustration of a giant stepladder, sometimes called a skyscraper stepladder, that is opened next to…
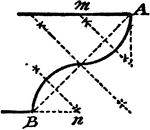
Construction Of A Talon
An illustration showing how to construct a talon, or two circle arcs that will tangent themselves, and…
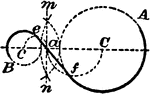
Construction Of Tangent Between 2 Circles
An illustration showing how to construct a tangent between 2 given circles. "Join the centers C and…
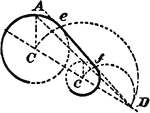
Construction Of Tangent To 2 Circles
An illustration showing how to construct a tangent to 2 given circles of different diameters. "Join…
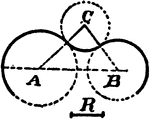
Construction Of Circle Tangent To 2 Circles
An illustration showing how to construct a tangent circle to 2 given circles. "Join centers C and c…
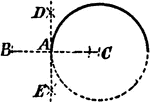
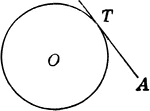
Construction Of Tangent To Circle
An illustration showing how to construct a tangent to a circle through a given point in a circumference.…
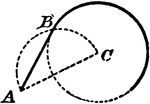
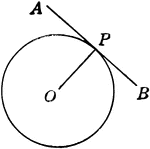
Construction Of Tangent To Circle
An illustration showing how to construct a tangent to a circle through a given point outside of a circumference.…
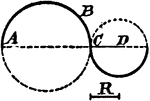
Construction Of Circle Tangent To Circle
An illustration showing how to construct a tangent circle to a circle with a given radius. "Through…
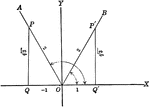
Trigonometric Reference Triangles/Angles (60 degrees) Drawn in Quadrants
Trigonometric reference triangles/angles drawn for 60 degree reference angel in quadrants I and II.

Trigonometric Reference Triangles/Angles Drawn in Quadrants
Trigonometric reference triangles/angles drawn for reference angel in quadrants I and II. This illustration…
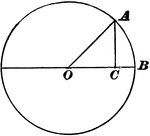
Trigonometry Triangle to Show Sine, Cosine, and Tangent
Right triangle OCA, inside of Circle O is used to show that side AC is "opposite" O and side OC is "adjacent"…
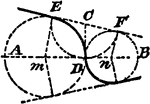
Construction Of Two Circles That Tangent Themselves and 2 Given Lines
An illustration showing how to construct two circles that tangent themselves and two given lines. "Draw…