Trigonometry: Triangles
This mathematics ClipArt gallery offers 42 images of right and oblique triangles that can be used with trigonometry problems involving solving triangles. There are also several images that can be used for application problems (crossing a river, lake, city block). For more triangles that can be used in trigonometry, see the Miscellaneous Triangles and Miscellaneous Right Triangles galleries.

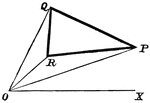
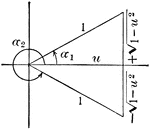
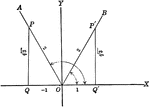
Coordinate Axis With Perpendiculars Drawn To Form Similar Right Triangles From Positive and Negative Theta, Θ
Angle XOP=Θ and angle XOQ=- Θ. From a point in the terminal side of each a perpendicular line is drawn…
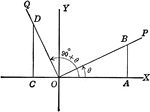
Coordinate Axis With Perpendiculars Drawn To Form Similar Right Triangles
Angle XOP=Θ and angle XOQ=90+Θ. From a point in the terminal side of each a perpendicular line is…
Angle Expressed As An Inverse Function
Illustration that can be used to show that when given an angle, expressed as an inverse function of…

Triangles and Sectors in Quadrant I
Illustration of an angle &alpha with the vertex at the center, O, of a circle with radius OB. AC and…
Triangle in Quadrant I
Illustration of an angle &alpha with the terminal side used to draw a triangle in quadrant I.
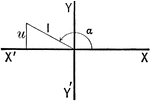
Triangle in Quadrant II
Illustration of an angle with the terminal side used to draw a triangle in quadrant II.
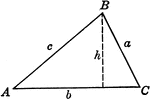
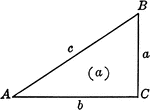
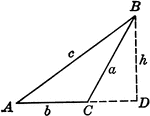
Triangle ABC With Height h
Triangle ABC with sides a,b,c labeled and angles A,B,C labeled and h labeled as height.
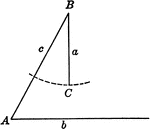
Ambiguous Case of Law of Sines Triangle
Illustration showing ambiguous case when the solution is not a triangle using law of sines.
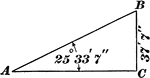
Triangle With Angle of 25 ° 33' 7" and Side of 37' 7"
Right triangle with angle of 25 ° 33' 7" and side of 37' 7"
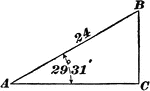
Triangle With Angle of 29 ° 31' and Side of 24
Right triangle with angle of 29 ° 31' and side of 24.
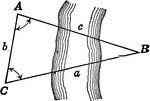
Oblique Triangle for Distance Across a River
Illustration of oblique triangle used to find distance across a river.
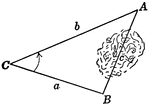
Oblique Triangle for Distance Across a River
Illustration of oblique triangle used to find distance across a river.
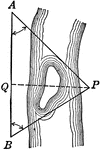
Oblique Triangle for Distance Across Lake
Illustration of oblique triangle used to find distance across a lake.
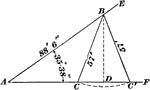
Oblique Triangle Used For Ambiguous Case
Oblique triangle with perpendicular drawn and angle of measure 35 ° 38" given, and sides of 88'…
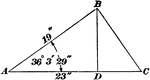
Oblique Triangle With Perpendicular Drawn
Oblique triangle with perpendicular drawn to form two right triangles, one with angle measuring 36 °…
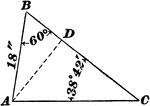
Oblique Triangle With Side 18" and Angles 60 ° and 38 ° 42'
Oblique triangle with side 18" and angles 60 ° and 38 ° 42'.
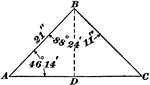
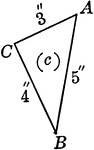
Oblique Triangle With Side 21' and Angles 88 ° 24' 11" and 46 ° 14'
Oblique triangle with side 21' and angles 88 ° 24' 11" and 46 ° 14'.
Obtuse Triangle ABC With Height h
Triangle ABC with sides a,b,c labeled and angles A,B,C labeled and h labeled as height.
Trigonometric Reference Triangles/Angles (60 degrees) Drawn in Quadrants
Trigonometric reference triangles/angles drawn for 60 degree reference angel in quadrants I and II.
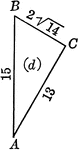
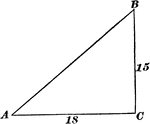
Right Triangle with leg 13 and hypotenuse 15
Right triangle ABC with angles A, B, C labeled and leg of 13 with hypotenuse of 15.
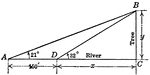
Right Triangle For Finding Distance Across a River
Right triangle ABC with angles A, B, C to be used for finding distance across a river. This is a trigonometry…
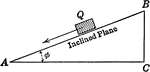
Inclined Plane Forming Right Triangle
Inclined plane forming right triangle showing the velocity of a body sliding a distance,s, down a smooth…
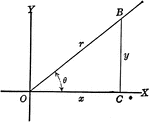
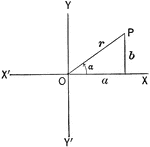
Right Triangle OCB With, x, y, and r shown
Right triangle OCB that can be used to show the relationships between x, y, r, and Θ.
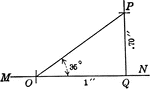
Right Triangle With Sides .7 and 1 and Angle of 35 degrees
Right triangle OQP with angle of 35 degrees, height of .70 inches, and leg of 1 inch.
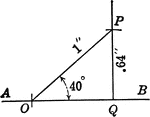
Right Triangle With Sides .64 and 1 and Angle of 40 degrees
Right triangle OQP with angle of 40 degrees, height of .64 inches, and hypotenuse of 1 inch.
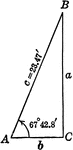
Right Triangle ABC With Angle 67 degrees 42.8 minutes and Hypotenuse 23.47 ft.
Right triangle ABC with a base angle of 67 degrees 4208 minutes and a hypotenuse of 23.47 ft.

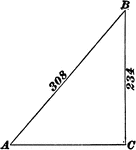
Right Triangle ABC With Leg 23.85 ft. and Hypotenuse 35.62 ft.
Right triangle ABC with a leg of 23.85 feet and a hypotenuse of 35.62 feet.
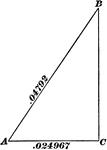
Right Triangle With Side .024967 and Hypotenuse .04792
Right triangle with side .024967 and hypotenuse .04792.
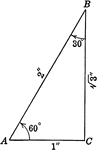
Special Right Triangle with Angles 30, 60, 90 degrees
Special right triangle with angles 30 degrees, 60 degrees, and 90 degrees with side measures/relationships…
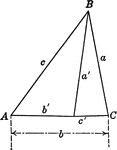
Triangles ABC and ABC'
Triangle ABC and triangle ABC'. This illustration could be used to demonstrate the law of sines.

Trigonometric Reference Triangles/Angles Drawn in Quadrants
Trigonometric reference triangles/angles drawn for reference angel in quadrants I and II. This illustration…
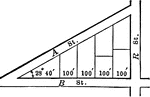
Triangular City Block With Angles and Lengths
Illustration showing an angle of 23 degrees 40 minutes making a triangle in a city block and marking…
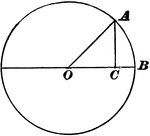
Trigonometry Triangle to Show Sine, Cosine, and Tangent
Right triangle OCA, inside of Circle O is used to show that side AC is "opposite" O and side OC is "adjacent"…