Bluffs, Other than Rocky
The typical representation of bluffs (other than rocky) on a topographical map.
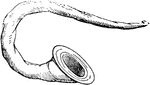
Curved buccina
"The buccina is curved for the convenience of the performer, with a very wide mouth, to diffuse…

Combination Horizontal Alignment/Intersection, Black and White
"The horizontal alignment Turn signs may be used in advance of situations where the horizontal roadway…

Combination Horizontal Alignment/Intersection, Color
"The horizontal alignment Turn signs may be used in advance of situations where the horizontal roadway…

Combination Horizontal Alignment/Intersection, Outline
"The horizontal alignment Turn signs may be used in advance of situations where the horizontal roadway…

Combination Horizontal Alignment/Intersection, Silhouette
"The horizontal alignment Turn signs may be used in advance of situations where the horizontal roadway…
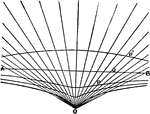
Conchoid
Illustration showing a conchoid, "a curve, shell-like in flexure (whence the name), invented by Nicomedes…

Contorted Rocks
"Curved and contorted rocks, near Old Head of Kinsale." — Encyclopedia Britannica, 1893
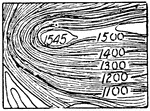
Contour System
In cartography, a contour line (often just called a "contour") joins points of equal elevation (height)…

Curvature of the Earth's Surface
If the earth were flat, as soon as an object appeared on the horizon we would see the upper and lower…
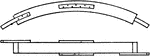
Curve in Pavement of Road
Illustration of blueprint used by highway engineers to widen the pavement on the inside of the curve…
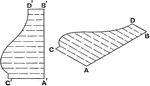
Drawing Irregular Isometric Curves of Solid
The illustration of an irregular curves for solid. The isometric projection of the curve can be drawn…
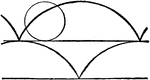
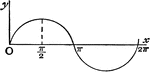
Cycloid
Illustration showing a cycloid curve. "The curve generated by a point in the plane of a circle when…
Cycloid
Illustration showing a cycloid curve. "The curve generated by a point in the plane of a circle when…
Cycloid
"A cycloid is the curve generated by the motion of a point on the circumference of a circle rolled along…

Cycloids
Illustration showing cycloid curves. "The curve generated by a point in the plane of a circle when the…
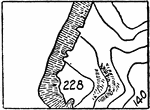
Depression Contours
The typical representation of depression contours, if otherwise ambiguous, on a topographical map.
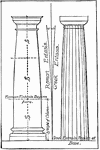
Entasis
"In architecture, the swelling or outward curve of the profile of the shaft of a column. Entasis. e…

Epicycloid
"In geometry, a curve generated by the motion of a point on the circumference of a circle which rolls…

Epicycloid and Hypocycloid
Epicycloid is generated by a circle rolled outside of another circle, whereas a hypocycloid is circle…
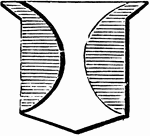
Flanche Ordinary
"Azure, a flanche, argent. The flanche is formed by two curved lines nearly touching each other in the…
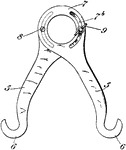
Butcher Gambrel
Bar, usually metal, with a central loop and a hook at each end, used to hang a carcass for butchering;…
Glacier Contours
In cartography, a contour line (often just called a "contour") joins points of equal elevation (height)…

Glacier Form Lines
In cartography, a contour line (often just called a "contour") joins points of equal elevation (height)…

Great Circle
A Great Circle is one which would be formed on the earth's surface by a plane passing through the earth's…
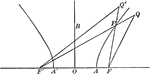
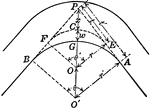
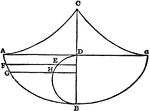
Foci Distance of Hyperbola
Illustration of a hyperbola with distances to foci drawn. "The difference of the distances of any point…
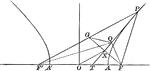
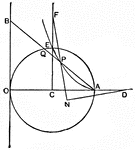
Line Bisecting Angle Between Focal Radii in Hyperbola
Illustration of a hyperbola with a line bisecting the focal radii. "If through a point P of an hyperbola…
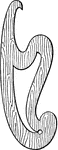
Irregular Curves
"Curves other than arcs of circles are drawn with the pencil or ruling pen by means of curved or irregular-shaped…
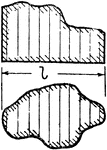
Area Of Irregular Figures
Illustration of an irregular figure. To find area, divide round curved portions in small steps with…
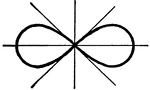
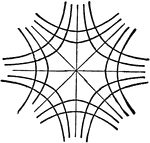
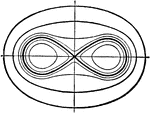
Lemniscate
A Lemniscate is, in general, a curve generated by a point moving so that the product of its distances…

Meridians and Parallels
The Meridian of any given place is that half of the meridian circle which passes through that place…
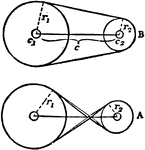
Pulley
Two arrangements of pulley: crossed belt and uncrossed belt. The pulleys are constructed with two circles…
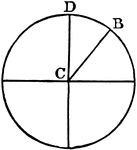
Sector
"In geometry: (a) A plane figure inclosed between the arc of a circle, ellipse, or other central curve…

Construction Of Shield's Anti-friction Curve
An illustration showing how to construct Shield's anti-friction curve. "R represents the radius of the…
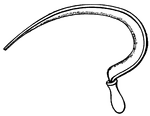
Sickle with Serrated Edge
"A reaping hook; a curved blade of steel (anciently also of bronze) having the edge on the inner side…